Induktor adalah elemen pasif yang berfungsi untuk menyimpan energi di dalam medan magnetik yang dimilikinya. Induktor digunakan di catu daya, transformer, radio, TV, radar dan motor listrik.
Sebuah induktor terdiri dari sebuah koil dan kawat yang menghantar arus (conductive wire). Jika arus melewati sebuah induktor, tegangan pada induktor proporsional dengan perubahan arus, persamaan tegangannya adalah sebagai berikut:
\(v=L\frac{di}{dt}\)………………………………………………(1)
L adalah induktansi, satuannya henry (H).
Induktansi dari induktor tegantung pada dimensi fisisnya, persamaan untuk menghitung induktansi dari induktor berbeda-beda tergantung dari bentuknya, seperti gambar di bawah ini adalah induktor berbentuk solenoid:
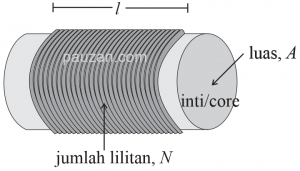
Gambar 1. Induktor berbentuk solenoid
Persamaan induktansi yang berbentuk solenoid adalah sebagai berikut:
\(L=\frac{N^2\mu A}{l}\)……………………………………….(2)
N adalah jumlah lilitan kawat, l adalah panjangnya lilitan, A adalah luasan di dalam lilitan kawat dan \(\mu\) adalah permeabilitas dari inti (core). Sedangkan lambang induktor dapat dilihat pada gambar berikut:
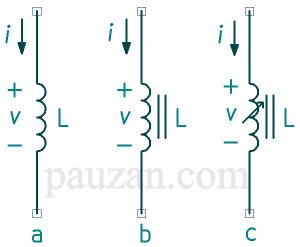
Gambar 2 Induktor dengan a). Core udara 3). Core besi 4). Core besi variabel
Persamaan 1 di atas dapat dirubah menjadi;
\(di=\frac{1}{L} v dt\)Diintegralkan;
\(i=\int_{-\infty}^{t} v(t) dt\)………………………………………….(3)
Persamaan di atas dapat juga ditulis;
\(i=(\int_{-\infty}^{t_0} v(t) dt+\int_{t_0}^{t} v(t) dt)\)……………………(4)
Berdasarkan persamaan (1), \(di=\frac{1}{L} v dt\) maka;
\(i=\frac{1}{L} \int v dt\)Jadi pada integral bagian \(-\infty\) sampai dengan \(t_0\) diperoleh arus, hasil integralnya sebagai berikut;
\(\int_{-\infty}^{t_0} v(t) dt=i(t_0)-i(-\infty)\)Pada waktu lampau yang tak terhingga, suatu konduktor pasti pernah arusnya nol maka \(i(-\infty)=0\) jadi yang tersisa adalah \(i(t_0)\), persamaan (4) menjadi;
\(i=\frac{1}{L} \int_{t_0}^{t} v(t) dt+i(t_0)\)……………………………..(5)
Konduktor menyimpan energi di dalam medan magnetiknya. Daya yang diterima oleh konduktor diperoleh dari persamaan (1) di atas;
\(p=vi=(L\frac{di}{dt})i\)……………………………………………………………(6)
Energi yang tersimpan di dalam konduktor adalah;
\(w=\int_{-\infty}^{t} p dt=\int_{-\infty}^{t} (L \frac{di}{dt})i dt\) \(w=L\int_{-\infty}^{t}i dt =\frac{1}{2}Li^2(t)-\frac{1}{2}Li^2(-\infty)\)Karena \(i(-\infty)=0\), maka;
\(w=\frac{1}{2}Li^2\)……………………………………………(7)
NOTE: berdasarkan persamaan (1) jika arusnya konstan (arus DC) maka tegangan bernilai 0, artinya jika konduktor dihubungkan dengan sumber DC maka akan bersifat sebagai terhubung pendek (short circuit).
Contoh soal 1
Tentukan arus yang melalui induktor 5 H jika tegangan yang melaluinya sebagai berikut:
\(v(t)=\left\{\begin{matrix} 30t^2, t>0 & \\ 0, t<0 & \end{matrix}\right.\)Berapakah energi yang tersimpan saat t=5 sekon?
Jawab
Berdasarkan persamaan (5), persamaan arus adalah;
\(i=\frac{1}{L} \int_{t_0}^{t} v(t) dt+i(t_0)\)Nilai L=5, dengan mengasumsi \(i(t_0)=0\), digunakan \(v(t)=30t^2\) karena yang ditanyakan saat \(t>0\) maka;
\(i=\frac{1}{5} \int_{t_0}^{t}30t^2 dt\) \(i=\frac{30}{5} \int_{t_0}^{t}t^2 dt=6 \frac{1}{3}t^3=2t^3 A\)Daya pada induktor;
\(p=vi=30t^2(20t^3)=60t^5\)Sehingga energi yang tersimpan pada induktor dari 0 sampai t=5 sekon adalah;
\(w=\int pdt\) \(w=\int_{0}^{5}60t^5dt=60\int_{0}^{5}t^5dt\) \(w=60[\frac{1}{6}t^6]_0^5=156,25 kJ\)
Contoh soal 2
Perhatikan rangkaian di bawah ini:
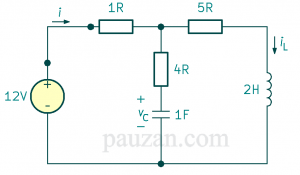
Gambar 3. Soal induktor
Jika dibawah tegangan DC, tentukanlah;
- \(i, v_c, i_L\)
- Energi yang tersimpan pada kapasitor dan induktor
Jawab
a. Menentukan \(i, v_c, i_L\)
Karena pada kondisi DC, maka kapasitor seperti sakelar terbuka dan induktor seperti sakelar tertutup, perhatikan rangkaian di bawah ini:
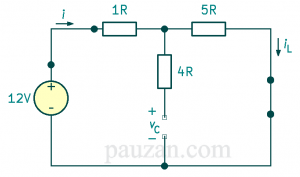
Gambar 4. Sifat kapasitor dan induktor pada sumber DC
Berdasarkan gambar 4, arus yang melalui induktor \(i_L\) dapat diperoleh dengan membagi tegangan 12 V dengan rangkaian seri 1 Ohm dengan 5 Ohm, kenapa 4 Ohm tidak dilibatkan? Karena ada rangkaian terbuka jadi arus dari 1 Ohm mengalir ke 5 Ohm. Jadi;
\(i_L=\frac{12}{1+5}=\frac{12}{6}=2 A \)Tegangan pada kapasitor \(v_c\);
Tegangangan \(v_c\) tersusun paralel dengan tegangan pada resistor 5 Ohm, ingat: karena rangkaian terbuka, 4 Ohm tidak diperhitungkan jadi seolah olah hanya ada kapasitor dengan 5 Ohm tersusun paralel.
\(v_c=v_{5ohm}=i_L 5=2 . 5 =10 V\)
b. Menghitung energi
Energi pada kapasitor dapat dihitung menggunakan persamaan;
\(w_c=\frac{1}{2}Cv_c^2=\frac{1}{2}1 . 10^2=50 J\)Energi yang tersimpan pada induktor adalah;
\(w_L=\frac{1}{2}Li_L^2=\frac{1}{2}2. 2^2=4 J\)