Bagaimana prinsip Kerja kapasitor?
Kapasitor terdiri dari dua pelat konduktor yang dipisahkan oleh bahan dielektrik, kapasistor adalah komponen pasif artinya komponen ini tidak memerlukan catu daya untuk bekerja. Jika kapasitor diberikan tegangan listrik seperti pada gambar 1, maka muatan positif akan berada pada pelat yang satu dan muatan negatif akan timbul pada pelat yang lainnya. Pada keadaan ini, kapasitor disebut menyimpan muatan listrik.

Gambar 1. Kapasitor yang diberi tegangan listrik
Banyaknya muatan yang disimpan ditulis sebagai , makin tinggi tegangan maka makin banyak muatan yang tersimpan. Persamaan yang menghubungkan dan adalah sebagai berikut:
\(q=Cv\) ……………………………………..(1)
\(C\) adalah kapasitansi dari kapasitor, kapasitansi adalah perbandingan antara muatan pada satu pelat dengan beda tegangan antara dua pelat, satuannya adalah farad (F). 1 farad=1 coulomb/volt.
Untuk memperoleh hubungan arus-tegangan pada kapasitor, kita turunkan persamaan 1 pada kedua ruas yaitu \(q\) diturunkan terhadap waktu dan \(v\) diturunkan terhadap waktu. Perlu diingat bahwa turunan \(q\) sebagai berikut:
\(i=dq/dt\)……………………………………….(2)
Maka penurunan kedua ruas pada persamaan (1) menjadi;
\(i=C\frac{dv}{dt}\)…………………………………………………(3)
Kapasitor yang memenuhi persamaan (3) disebut sebagai kapasitor linier. Hubungan antara arus dengan tegangan pada persamaan 3 dapat dilihat pada gambar di bawah ini:

Gambar 2. Hubungan \(i \) dan \( v \)
Hubungan arus-tegangan diperoleh dari mengintegralkan kedua ruas terhadap waktu pada persamaan (3), maka diperoleh:
\( idt=C \frac{dv}{dt} dt \)\(\int_{t_0}^{t} idt=C(v_t-v_{t_0}) \)
Karena \( v_t=v\) maka;
\( v-v_{t_0}=\frac{1}{C} \int_{t_0}^{t}idt \)\( v=\frac{1}{C} \int_{t_0}^{t}idt+v_{t_0} \)……………………………………(4)
Dimana \( v_{t0}=\frac{q(t_0)}{C}\). Persamaan 4 menunjukkan bahwa tegangan kapasitor tergantung pada keadaan arus sebagai fungsi waktu.
Sedangkan daya yang diberikan ke kapasitor adalah:
\( p=vi\)Dengan mensubtitusikan persamaan (3) maka;
\( p=Cv \frac{dv}{dt} \) ……………………………………………………….(5)
Oleh karena itu energi yang tersimpan di dalam kapasitor adalah:
\( w=\int_{-\infty}^{t}pdt=C\int_{-\infty}^{t}v\frac{dv}{dt}dt=C\int_{-\infty}^{t}v dv \)\( w=\frac{1}{2}Cv(t)^2-\frac{1}{2}Cv(-\infty)^2 \)
\( v(-\infty)=0 \) karena pada saat \( t=-\infty \) kapasitor tidak memiliki muatan maka:
\( w=\frac{1}{2} Cv^2 \)……………………………………………(6)
Karena \( q=cv \) maka \( v^2=\frac{q^2}{C^2} \), persamaan (6) menjadi;
\( w=\frac{1}{2} C \frac{q^2}{C^2}=\frac{1}{2}\frac{q^2}{C} \)\( w=\frac{q^2}{2C} \)…………………………………………(7)
Beberapa catatan penting yang diperoleh dari kapasitor:
- Berdasarkan persamaan (3) jika tegangan yang melalui kapasitor tidak berubah-ubah terhadap waktu (seperti sumber DC) maka arus yang melalui kapasitor adalah nol, oleh karena itu: Kapasitor bersifat rangkaian terbuka pada sumber DC. Perlu diingat bahwa jika baterai DC dihubungkan ke kapasitor maka kapasitor akan terisi muatan.
- Tegangan pada kapasitor tidak dapat berubah secara instan (tiba-tiba), perhatikan gambar di bawah ini:
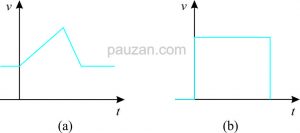
Gambar 3 (a). perubahan tegangan yang diperbolehkan (b) perubahan \(v\) yang tidak mungkin terjadi pada kapasitor
Contoh Soal 1
- Tentukan muatan yang tersimpan pada kapasitor 3 pF dimana dilalui oleh 20V
- Hitunglah energi yang tersimpan pada kapasitor tersebut
Jawab
- Karena \( q=Cv \), maka;
\( q=3 . 10^{-12} . 20=60 \) pC
- \( w=\frac{1}{2}Cv^2 \)
\( w=\frac{1}{2} . 3 .10^{-12} . 400=600 \) pJ
Contoh Soal 2
Tegangan yang melalui kapasitor 5 μF adalah sebagai berikut:
\( v(t)=10 \cos 6000t \) V
Berapakah arus yang melaluinya?
Jawab
\( i=C \frac{dv}{dt}=5 . 10^{-6}\frac{d}{dt} (10 \cos 6000t) \) \( i=5 . 10^{-6} . 10\frac{d}{dt}(\cos 6000t) \)Karena
\( \frac{d(\cos \alpha t)}{dt}=-\alpha \sin \alpha t \)Maka;
\( i=5 . 10^{-6} . 10 (-6000 \sin 6000t )=-0,3 \sin 6000t \) A
Contoh Soal 3
Tentukan arus yang melalui kapasitor 200 μF dimana tegangan pada kapasitor tersebut dapat dilihat pada gambar di bawah ini:
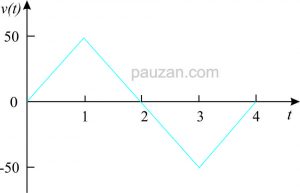
Gambar 4. Tegangan pada kapasitor
Jawab
Berdasarkan gambar di atas, tegangan pada kapasitor dapat ditulis sebagai berikut:
\(v(t)=\left\{\begin{matrix} 50 t & 0<t<1\\ 100-50t&1<t<3 \\ -200+50t&3<t<4 \\ 0& tempat lain \end{matrix}\right.\)Persamaan arus adalah;
\( i=C\frac{dv}{dt} \)Maka tiap persamaan tegangan diturunkan terhadap waktu dan dimasukkan nilai \( C \), persamaan arusnya adalah;
\(i(t)=200\times10^{-6}\left\{\begin{matrix} 50& 0<t<1\\ -50&1<t<3 \\ 50&3<t<4 \\ 0& tempat lain \end{matrix}\right.\)Dikalikan dengan \( C \) maka;
\(i(t)=\left\{\begin{matrix} 10& 0<t<1\\ -10&1<t<3 \\ 10&3<t<4 \\ 0& tempat lain \end{matrix}\right.\)Berdasarkan persamaan arus di atas, kita dapat menggambar bentuk gelombangnya, diperoleh:
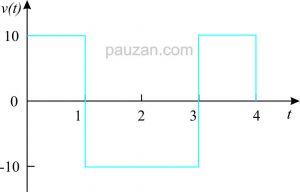
Gambar 5. Bentuk arus dari kapsitor 200 μF
Contoh Soal 4
Perhatikan gambar berikut ini:
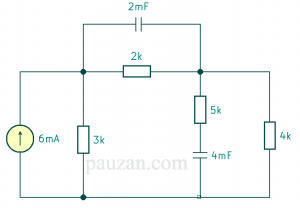
Gambar 6. Rangkaian yang terdapat kapasitor
Berdasarkan gambar di atas, hitunglah energi yang tersimpan pada tiap kapasitor dimana rangkaiannya dialiri arus DC.
Jawab
Perhatikan bahwa kapasitor dalam rangkaian DC menjadi seperti rangkaian terbuka, artinya tidak dapat mengalirkan arus. Jadi skema rangkaian pada soal di atas menjadi;
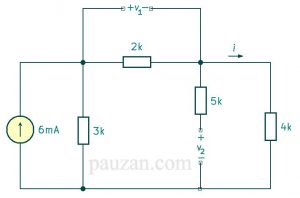
Gambar 7. Setelah kapasitor diganti menjadi rangkaian terbuka
Berdasarkan gambar 7, arus yang melalui 2 k dan 4 k adalah sama, tapi dari simpul antara sumber 6mA, 2k dan 3k arus mulai terbagi ke 3k dan 2k (dan terus mengalir ke 4k). jadi dengan menggunakan rangkaian pembagi arus maka arus yang melalui 2k dan 4k dapat diketahui:
Tegangan total rangkaian adalah:
\( v=i_{tot} R \)\( R \) disini adalah resistensi eqivalen, yaitu diperoleh dari 2k dan 4k disusun seri, hasilnya 6k. selanjutnya 6k tersusun paralel dengan 3k, maka resistensi eqivalennya adalah:
\( \frac{1}{R}=\frac{1}{3k}+\frac{1}{6k}=\frac{(2+1)}{6k}=\frac{3}{6k} \)\( R=2k \)
Jadi tegangan total pada rangkaian di atas:
\( v=i_{tot} 2k \)Selanjutnya dicari arus yang melalui 6k (hasil seri 2k dan 4k);
\( i=\frac{v}{6k}\)Karena tersusun paralel maka tegangannya sama dengan tegangan total, persamaan arus menjadi;
\( i=\frac{(i_{tot} 2k)}{6k}=i_{tot}\frac{1}{3}=6mA \times \frac{1}{3}=2 \) mA
Karena 6k berasal dari rangkaian seri antara 2k dan 4k maka arus yang melalui 2k dan 4k juga sama yaitu sebesar 2 mA.
Perhatikan pada gambar 7 bahwa pada kapasitor pertama sama dengan tegangan pada kaki-kaki 2k, jadi:
\( v_1=i\times2k=2 mA \times 2k=4 \) V
Sedangkan tegangan pada kapasitor kedua sama saja dengan tegangan pada resistor 4k, kenapa 5k tidak dianggap? Karena rangkaian terbuka jadi mau ada atau tidak ada 5k arus tidak akan melewatinya, arus pasti akan selalu menuju 4k. jadi tegangan pada kapasitor kedua:
\( v_2=i\times 4k=2 mA \times 4k=8 \) V
Energi yang tersimpan pada tiap kapasitor adalah:
\( w_1=\frac{1}{2} C_1 v_{1}^{2}=\frac{1}{2} \times 2 \times 10^{-3}\times(4)^2=16 \) mJ
\( w_2=\frac{1}{2}C_2 v_2^2=\frac{1}{2}\times4\times10^{-3}\times(8)^2=128 \) mJ