Jika rangkaian seri RC tiba-tiba diberikan sumber arus atau sumber tegangan, maka sumber tersebut dapat dimodelkan sebagai fungsi step dan respon dari rangkaian disebut sebagai respon step dari rangakaian RC. Perhatikan rangkaian RC pada gambar 1a dan rangkaian eqivalennya pada 1b.
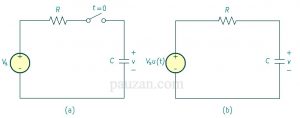
Gambar 1(a)Rangkaian RC (b)dan rangkaian eqivalennya
\( V_s \) adalah sumber tegangan dengan nilai tetap, kemudian dipilih tegangan kapasitor sebagai respon rangakaian yang akan dicari. Kita bisa mengasumsikan tegangan awal pada kapasitor (kondisi rangkaian masih terbuka) sebagai \( V_0 \) :
\( v(0^{-} )=v(0^{+} )=V_0 \)………………………………………….(1)
\( v(0^{-}) \) adalah tegangan pada kapasitor sesaat sebelum sakelar tertutup dan \( v(0^{+}) \) adalah tegangan sesaat setelah sakelar tertutup.
Selanjutnya kita terapkan hukum arus Kirchhoff (KCL) pada sakelar sesaat setelah dihubungkan dengan kapasitor. Arus masuk pada sakelar berasal dari arus yang mengalir melalui resistor sedangkan arus keluar dari sakelar adalah arus yang menuju kapasitor, maka KCLnya adalah:
\( i_{masuk}=i_{keluar} \)\( i_{resistor}=i_{kapasitor} \)
Tegangan pada resistor adalah pengurangan tegangan sumber \( V_s u(t) \) oleh tegangan kapasitor, dengan menggunakan hukum Ohm diperoleh;
\( i_{masuk}=\frac{V_s u(t)-v}{R} \)………………………………..(2)
Sedangkan arus pada kapasitor memenuhi persamaan:
\( i_{keluar}=C \frac{dv}{dt} \)Maka KCL menjadi:
\( \frac{V_s u(t)-v}{R}=C \frac{dv}{dt} \)Persamaan arus pada resistor dipindah ruas ke kanan:
\( 0=C\frac{dv}{dt}-(\frac{V_su(t)-v}{R}) \)\( C \frac{dv}{dt}-(\frac{V_su(t)-v}{R})=0 \)
\( C\frac{dv}{dt}+\frac{v-V_su(t)}{R}=0 \)
\( C\frac{dv}{dt}+\frac{v}{R}=\frac{V_su(t)}{R} \)
Dikali 1/C maka;
\( \frac{dv}{dt}+\frac{v}{RC}=\frac{V_s}{RC}u(t)\)…………………………………….(3)
Ingat v adalah tegangan pada kapasitor. Jika t>0 nilai dari fungsi step u(t)=1 maka persamaan (3) menjadi;
\( \frac{dv}{dt}+\frac{v}{RC}=\frac{V_s}{RC} \)………………………….(4)
v/RC dipindah ruas ke kanan maka;
\( \frac{dv}{dt}=-\frac{v}{RC}+\frac{V_s}{RC} \)\( \frac{dv}{dt}=-(\frac{v-V_s}{RC}) \)
dt pindah ruas ke kanan;
\( \frac{dv}{v-V_s}=-\frac{dt}{RC} \)………………………………………(5)
Kita integralkan kedua ruas:
Ruas kiri:
\( \int_{V_0}^{v(t)}\frac{dv}{v-V_s} \)Ingat:
\( \int \frac{dx}{x}=\ln x \)Maka kita bisa buat permisalan: \( x=v-V_s \), maka \( dx=dv \). Jadi integral pada ruas kiri menjadi:
\( \int_{V_0}^{v(t)}\frac{dv}{v-V_s}=\int \frac{dx}{x}=\ln x \)Kita kembalikan lagi ke besaran yang sebenarnya:
\(\ln (v-V_s)|_{V_0}^{v(t)}=\ln (v(t)-V_s)-\ln (V_0-V_s)\)
Ingat \(\ln a-\ln b=\ln a/b\) maka;
\( \int_{V_0}^{v(t)}\frac{dv}{v-V_s}=\ln {\frac{v(t)-V_s}{V_0-V_s}} \)
Ruas kanan:
\( \int_{0}^{t}-\frac{dt}{RC}=-\frac{t}{RC}|_0^t \)\( \int_{0}^{t}-\frac{dt}{RC}=-\frac{t}{RC} \)
Persamaan (5) menjadi:
\( \ln {\frac{v(t)-V_s}{V_0-V_s}}=-\frac{t}{RC} \)Kita rubah ke bentuk e, ingat:
\( e^{\ln a}=a \)Maka;
\( \frac{v(t)-V_s}{V_0-V_s}=e^{-t/RC} \)Konstanta waktu rangkaian RC adalah τ=RC maka;
\( \frac{v(t)-V_s}{V_0-V_s}=e^{-t/\tau} \)\( v(t)-V_s=(V_0-V_s)e^{-t/\tau} \)
\( v(t)=V_s+(V_0-V_s)e^{-t/\tau}, t>0 \)…………………….(6)
Oleh karena itu secara umum persamaan tegangan pada kapasitor adalah:
\(v(t)=\left\{\begin{matrix} V_0, &t<0 \\ V_s+(V_0-V_s)e^{-t/\tau}, &t>0 \end{matrix}\right.\)……..(7)
Persamaan di atas disebut juga sebagai respon total dari rangkaian RC yang diberikan sumber tegangan DC secara tiba-tiba. Dengan mengasumsikan bahwa \( V_s>V_0 \) maka grafik yang diperoleh dari persamaan (7) adalah sebagai berikut:
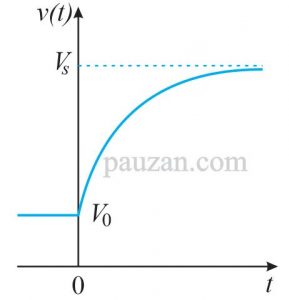
Gambar 2. Respon dari rangkaian RC dimana tegangan mula-mula kapasitor sebesar \( V_0 \)
Sekarang jika kita asumsikan bahwa pada kondisi awal, kapasitor tidak bermuatan maka \( V_0=0 \), persamaan (7) menjadi:
\(v(t)=\left\{\begin{matrix} 0, &t<0 \\ V_s(1-e^{-t/\tau}), &t>0 \end{matrix}\right.\)………….(8)
Mengingat sungsi step u(t) adalah:
\(u(t)=\left\{\begin{matrix} 0, &t<0 \\ 1, &t>0 \end{matrix}\right.\)
Maka persamaan (8) bisa ditulis menjadi:
\( v(t)=V_s(1-e^{-t/\tau})u(t) \)……………………………………(9)
Persamaan (9) di atas adalah respon total dari rangkaian RC untuk kasus kondisi awal kapasitor adalah tak bermuatan.
Berapakah besar arus yang melalui kapasitor? Arus pada kapasitor dapat dicari menggunakan persamaan:
\( i(t)=C\frac{dv}{dt} \)Kita gunakan persamaan tegangan (persmaan 7) maka diperoleh:
\( i=C\frac{d}{dt}(V_s(1-e^{-t/\tau}))=C\frac{dV_s}{dt}-CV_s\frac{d}{dt}e^{-t/\tau} \)Ingat:
\( \frac{d}{dx}e^{ax}=ae^{ax} \)maka:
\( i=0-CV_s(-\frac{1}{\tau})e^{-t/\tau} \)\( i=\frac{C}{\tau}V_se^{-t/\tau} \)
Bisa juga ditulis ke bentuk fungsi step :
\( i=\frac{C}{\tau}V_se^{-\frac{t}{\tau}}u(t) \)τ=RC maka;
\( i=\frac{C}{RC}V_se^{-\frac{t}{\tau}}u(t) \)
\( i=\frac{V_s}{R}e^{-t/\tau}u(t) \)………………………….(10)
Gambar di bawah ini adalah kurva tegangan dan arus untuk kapasitor dengan kondisi awal tanpa muatan.
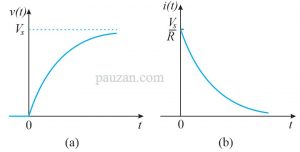
Gambar 3. (a)Tegangan dan (b) arus pada kapasitor dengan kondisi awal tak bermuatan
Selain cara di atas, untuk mengetahui respon total dari rangkaian RC adalah dengan membagi keadaan pada rangkaian menjadi dua yaitu respon sementara (transien) dan respon permanen (steady state).
Respon total=respon transien+respon steady state
secara matematis dapat ditulis:
\( v=v_t+v_{ss} \)…………………………………………..(11)
\( v_t \) adalah respon transien, persamaannya:
\( v_t=(V_0-V_s)e^{-t/\tau} \)…………………………………..(12)
Perhatikan bahwa berdasarkan persamaan (12) dapat disimpulkan bahwa respon transien adalah respon dari rangkaian yang bersifat sementara dan akan hilang seiring dengan berjalannya waktu.
Sedangkan \( v_{ss} \) adalah respon steady-state, rumusnya:
\( v_{ss}=V_s \)………………………………….(13)
Berdasarkan persamaan (13), dapat disimpulkan bahwa respon steady-state adalah karakteristik dari rangkaian setelah diberikan sumber tegangan DC dimana sumber tersebut sudah diberikan untuk jangka waktu yang sudah lama.
Dengan menggunakan konsep transien dan steady-state, persamaan (6) dapat ditulis sebagai berikut:
\( v(t)=v(\infty)+[v(0)-v(\infty)]e^{-t/\tau} \)……………………….(14)
\( v(0) \) adalah kondisi awal sesaat setelah sumber tegangan dihubungkan ke kapasitor, \( v(\infty) \) adalah tegangan akhir dari kapasitor atau tegangan pada kondisi steady-state.
Jika keadaan sakelar berubah dari off ke on terjadi pada \( t=t_0 \) bukan pada t=0, maka terjadi perlambatan waktu respon pada rangkaian. Persamaan (13) menjadi:
\( v(t)=v(\infty)+[v(t_0)-v(\infty)]e^{-\frac{t-t_0}{\tau}} \)………………(15)
Dimana \( v(t_0) \) adalah tegangan mula-mula saat \( t=t_0^+ \) sedangkan \( v(\infty) \) adalah tegangan pada kondisi steady-state.
Contoh Soal 1
Perhatikan rangkaian di bawah ini.
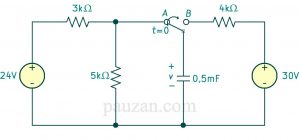
Gambar 4. Contoh soal respon step rangkaian RC
Sakelar berada pada posisi A sudah dalam jangka waktu yang lama. Pada waktu t=0, sakelar berpindah ke B. Tentukanlah \( v(t) \) untuk t>0 dan hitunglah nilainya pada t=1 sekon dan t=4 sekon.
Jawab
Saat \( t<0 \)
Pada saat t<0 sakelar pada posisi A, artinya kapasitor terhubung langsung dengan sumber DC 24 V. kapasitor tersusun paralel dengan resistor 5kΩ maka tegangan pada kapasitor sama besarnya dengan tegangan pada resistor tersebut.
Untuk mencari tegangan pada resistor 5kΩ digunakan konsep rangkaian pembagi tegangan:
\( v_{5k}=\frac{5k}{3k+5k}v_{input} \)\( v_{5k}=\frac{5}{8} 24 =15 V \)
Maka tegangan pada kapasitor saat t<0 15 V, karena tegangan tidak bisa berubah dengan cepat maka tegangan sesaat sebelum sakelar dipindah ke posisi B, \( v(0^-) \) dan sesaat setelah dipindah ke posisi B, \( v(0^+) \) sama besarnya dengan tegangan pada saat t=0, maka:
\( v(0)=v(0^-)=v(0^+)=15 V \)
Saat \( t>0 \)
Pada saat t>0 sakelar berada pada posisi B maka sekarang kapasitor terhubung dengan sumber tegangan \( V_s \) =30 V. berapakah tegangan steady-state kapasitor? Perhatikan rangkaian di bawah ini:
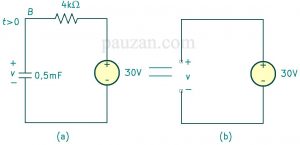
Gambar 5. Tegangan kapasitor sama dengan sumber tegangan 10V
Saat steady state kapasitor bersifat rangkaian terbuka maka tidak ada arus mengalir shg ada tidaknya resistor 4k tidak ada pengaruhnya sehingga sama saja dengan mengatakan bahwa tegangan pada kapasitor sama dengan sumber tegangan. Maka tegangan steady-state kapasitor adalah \( v(\infty)=V_s=30 V \). kita akan mencari persamaan v pada kapasitor sesuai dengan persamaan (13):
\( v(t)=v(\infty)+[v(0)-v(\infty)]e^{-t/\tau} \)
Berdasarkan persamaan di atas, besaran yang belum diketahui adalah konstanta waktu τ untuk rangkaian RC, rumusnya adalah:
\( \tau=RC \)
R runggal yang terhubung seri dengan kapasitor adalah resistor 4kΩ, maka konstanta waktunya adalah:
\( \tau=4\times 10^3 . 0,5 \times 10^{-3}=2 sekon \)Persamaan tegangannya menjadi:
\( v(t)=30+[15-30] e^{-t/2} \)
Untuk t=1
\( v(1)=30+[15-30] e^{-1/2} \) \( v(1)=30-15e^{-1/2}=20,9 V \)
Untuk t=4
\( v(4)=30+[15-30] e^{-4/2} \) \( v(4)=30-15e^{-2}=27,97 V \)
Contoh Soal 2
Perhatikan rangkaian berikut ini:
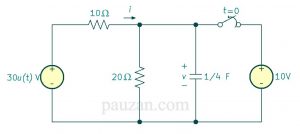
Gambar 6. Contoh soal respon step rangkaian RC
Sakelar sudah tertutup dalam jangka waktu yang lama dan dibuka saat t=0. Tentukanlah i dan v untuk waktu yang lama.
Jawab
Fungsi step pada sumber tegangan sebelah kiri adalah:
\(30u(t)=\left\{\begin{matrix} 0, & t<0\\ 30, & t>0 \end{matrix}\right.\)
Untuk t<0
Pada saat t<0, sakelar tertutup maka \( 30u(t)=0 \) maka pada saat t<0 sumber tegangan dapat diganti dengan rangkaian pendek (short circuit). Selain itu, karena sakelar sudah dalam kondisi tertutup dalam waktu yang lama maka tegangan kapasitor sudah mencapai steady-state sehingga kapasitor bersifat sebagai rangkaian terbuka. Perhatikan gambar berikut ini:
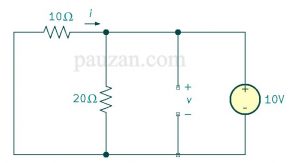
Gambar 7. Saat t<0 dan kapasitor dalam steady-state
Berdasarkan gambar di atas, tegangan pada kapasitor adalah paralel dengan sumber tegangan maka:
\( v(0^-)=10 V \)Karena tegangan pada kapasitor tidak dapat berubah dengan instan maka \( v(0^- )=v(0)=v(0^+) \) maka;
\( v(0)=10 V \)
Untuk \( t>0 \)
Saat t>0 sakelar terbuka sehingga sumber tegangan 10 V terputus, pada saat itu juga sumber tegangan \( 30u(t)=30 V \). Rangkaian untuk kasus t>0 dapat dilihat pada gambar berikut ini:
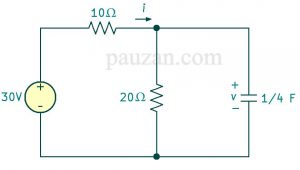
Gambar 8. Saat t>0
Untuk jangka waktu yang lama, kapasitor mencapai steady-state artinya kapasitor bersifat sebagai rangkaian terbuka, sehingga tegangannya pada kondisi steady-state adalah sama besarnya dengan tegangan pada resistor 20Ω, karena kapasitor dan resistor 20Ω tersusun paralel. Dengan menggunakan konsep pembagi tegangan, tegangan pada resistor 20Ω atau pada kapasitor sebesar:
\( v(\infty)=\frac{20}{20+10}30=20 V \)
Selanjutnya kita merubah bentuk rangkaian pada soal menjadi hanya satu R (artinya kita cari \( R_{th}\)). Kenapa? Karena rangkaiannya akan dirubah ke bentuk RC seperti pada gambar 1 di atas. Dengan menerapkan teorema thevenin dalam menentukan \( R_{th} \), maka langkah-langkahnya:
Sumber tegangan 30V dimatikan, menjadi rangkaian pendek (short circuit) seperti pada gambar berikut:
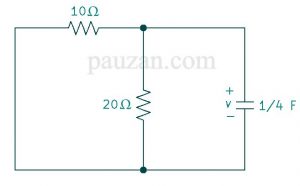
Gambar 9. Sumber tegangan dimatikan untuk mendapatkan \( R_{th} \)
Berdasarkan gambar 9, resistansi eqivalennya (bisa juga disebut resistansi Thevenin) diperoleh dari paralel antara 10Ω dan 20Ω:
\( \frac{1}{R_{th}}=\frac{1}{10}+\frac{1}{20}=\frac{2+1}{20} \)\( R_{th}=\frac{20}{3} \Omega \)
Karena sudah diperoleh R tunggal dan C maka konstanta waktunya adalah:
\( \tau=R_{th}C=\frac{20}{3} \frac{1}{4}=\frac{5}{3} sekon \)
Maka tegangan kapasitor adalah:
\( v(t)=v(\infty)+[v(0)-v(\infty)]e^{-t/\tau} \) \( v(t)=20+[10-20]e^{-\frac{t}{5/3}} \)\( v(t)=20-10e^{-0,6t} \)
Mencari \( i \)
Perhatikan gambar 8b, arus i yang mengalir adalah penjumlahan antara arus pada kapasitor dan resistor 20Ω:
\( i=\frac{v_{20\Omega}}{R}+C\frac{dv}{dt} \)\( i=\frac{20-10e^{-0,6t}}{20}+\frac{1}{4}\frac{d}{dt}(20-10e^{-0,6t}) \)
\( i=1-0,5e^{-0,6t}+\frac{1}{4}(-0,6)(-10)e^{-0,6t} \)
\( i=(1-e^{-0,6t}) A \)
Sekarang kita tulis ulang persamaan v dan i yang diperoleh dari soal di atas:
\(v=\left\{\begin{matrix} 10V, & t<0\\ 20-10e^{-0,6t} V, & t>0 \end{matrix}\right.\)\(i=\left\{\begin{matrix} -1 A, & t<0\\ 1+e^{0,6t} A, & t>0 \end{matrix}\right.\)
PREVIOUS: fungsi singularitas
NEXT: Respon Step Rangkaian RL