Analisis Mesh adalah analisis yang dibangun dari penggunaan Hukum Ohm dan KVL (Hukum Tegangan Kirchhoff). Analisis ini bertujuan untuk menghitung arus yang tidak diketahui. Kita mulai pembahasan dari mesh, mesh merupakan loop, pada loop tersebut tidak ada loop lain terkandung di dalamnya. Perhatikan gambar di bawah ini:
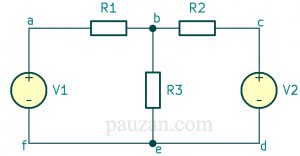
Gambar 1. Rangkaian yang terdiri dari dua mesh
Dari gambar 1, jalur abefa adalah rangkaian tertutup maka kita bisa membuat loop di dalamnya, begitu juga dengan jalur bcdeb. Perhatikan gambar berikut:
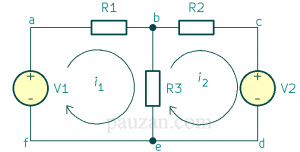
Gambar 2. Loop yang terbentuk
Berdasarkan gambar 2, jalur abcdefa tidak bisa membentuk mesh karena di dalam jalur tersebut terdapat dua loop. Jalur abefa dan bcdeb membentuk loop maka masing-masing loop membentuk mesh. Loop 1 menghasilkan arus mesh 1 (ditulis \(i_1\)) dan loop 2 menghasilkan arus mesh \(i_2\). Arah arus mesh mengikuti arah loop, searah jarum jam. Jika sudah diperoleh arus mesh maka kita bisa menghitung arus sebenarnya pada suatu rangkaian listrik.
Langkah mengerjakan analisis Mesh:
- Buatlah loop pada rangkaian tertutup, jika lebih dari satu loop maka beri indeks loop1, loop2, dan seterusnya.
- Dari tiap loop akan menghasilkan satu arus mesh. Arus mesh memiliki simbol \(i_1\) , jika dalam suatu rangkaian terdapat lebih dari satu arus mesh maka diberi indeks \(i_1\) untuk arus mesh 1, begitu seterusnya.
- Analisis tiap arus mesh menggunakan KVL
SOAL
Perhatikan gambar di bawah, tentukan arus \(I_1, I_2\) dan \(I_3\)menggunakan analisis Mesh. Catatan: 5R berarti 5 Ohm, begitu juga dengan 6R, 10R dan 4R.
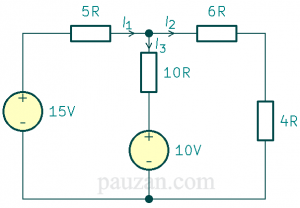
Gambar 3. Soal analisis mesh
Berdasarkan rangkaian di atas, terdapat dua loop (dari dua rangkaian tertutup) maka terdapat dua mesh sehingga terdapat dua arus mesh. Kedua arus mesh tersebut dapat dilihat pada gambar berikut:
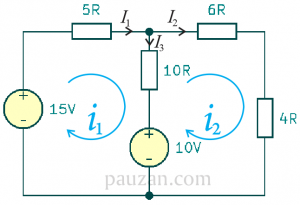
Gambar 4. Dua arus mesh yang terbentuk
Arus mesh 1 (\(i_1\)):
Terapkan KVL:
\(ΣV=0\)
Loop pertama kali menemui tanda negatif (-) pada sumber tegangan 15V, maka ditulis -15. Tanda positif pada 10V maka ditulis +10. Sehingga KVL pada \(i_1\) menjadi:
\(-15+5i_1+10i_1-10i_2+10=0\)
\(5i_1\) adalah tegangan diantara dua kaki resistor 5 Ohm. Arus yang melalui resistor 5 Ohm adalah arus mesh \(i_1\) sehingga tegangan pada resistor tersebut (hukum Ohm: \(V=IR\) sebesar \(V=i_15\) .\(10i_1\) dan \(-10i_2\) juga diperoleh dengan cara yang sama. \(-10i_2\) bernilai negatif karena \(i_2\) berlawanan arah dengan \(i_1\). Persamaan di atas menjadi:
\(-5+15i_1-10i_2=0\)
\(15i_1-10i_2=5\)
Dibagi 5
\(3i_1-2i_2=1\)
\(i_2=(3i_1-1)/2\)…………………..(1)
Arus mesh \(i_2\)
Menerapkan KVL:
\(-10+10i_2-10i_1+6i_2+4i_2=0\)
\(-10i_1+20i_2=10\)
Dibagi 10
\(-i_1+2i_2=1\)…………………….(2)
Subtitusi persamaan (1) di atas, maka:
\(-i_1+2((3i_1-1)/2)=1\)
\(-i_1+3i_1-1=1\)
\(i_1=1 A\)
Jadi besar \(i_2\) adalah:
\(i_2=(3 .1-1)/2=1 A\)
Hubungan arus sebenarnya dengan arus mesh
\(I_1\) memiliki arah dan besar sama dengan \(i_1\),maka \(I_1=1A\).
\(I_2\) memiliki besar dan arah yang sama dengan \(i_2\), maka:
\(I_2=i_2\)
\(I_2=1 A\)
\(I_3\) berarah ke bawah pada resistor 10 Ohm, hubungannya dengan arus mesh adalah:
\(I_3=i_1-i_2\)
Masukkan \(i_1\) dan \(i_2\) maka;
\(I_3=1-1=0 A\)
Jadi \(I_1\)=1 A, \(I_2\)=1 A dan \(I_3\)=0