Pada analisis mesh tanpa sumber arus, kita cukup mengaplikasikan Hukum Ohm dan KVL (Hukum Tegangan Kirchhoff). Namun jika dalam suatu rangkaian terdapat sumber arus maka analisis Meshnya terdapat sedikit perbedaan. Pada umumnya analisis dengan sumber arus terbagi menjadi dua:
- Sumber arus hanya ada pada satu mesh
- Sumber arus berada di antara dua mesh
Sumber arus hanya pada satu mesh
Untukkasus ini, besarnya arus mesh sama dengan besar sumber arus. Perhatikan rangkaian berikut:
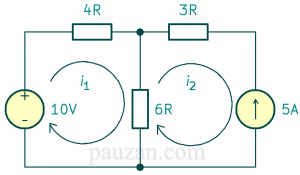
Gambar 1. Sumber arus pada satu mesh
Berdasarkan gambar di atas, sumber arus \(5A\) hanya berada pada mesh 2. Besarnya arus mesh \(i_2\) sama dengan 5A tapi berlawanan arah maka \(i_2=-5A\).
Sumber arus berada di antara dua mesh
Perhatikan rangkaian di bawah ini:
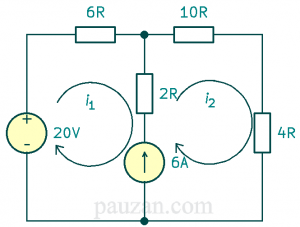
Gambar 2. Sumber arus berada diantara dua mesh
Berdasarkan gambar 2, sumber arus \(6A\) berada diantara mesh 1 dan 2. Untuk kasus seperti ini, sumber arus tersebut dan komponen lain (jika ada) yang tersusun seri dengannya dihilangkan, kondisi seperti ini yang disebut sebagai supermesh. Kkarena terjadi supermesh, Gambar 2 di atas berubah menjadi:
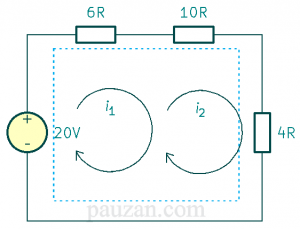
Gambar 3. Supermesh yang terbentuk dari dua mesh
Langkah-langkah menyelesaikan rangkaian yang terdapat supermesh:
- Buat supermesh
- Terapkan KVL pada supermesh
- Terapkan KCL (Hukum Arus Kirchhoff) pada simpul dimana sumber arus dan arus mesh bertemu
- Hitung arus tiap mesh
- Hitung arus yang ditanyakan
SOAL
Tentukan arus \(I_1, I_2\) dan \(I_3\) pada rangkaian berikut:
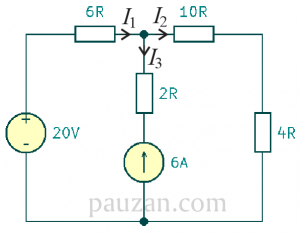
Gambar 4. Soal supermesh
Buat Supermesh:
Dari soal di atas, sumber arus berada diantara dua mesh, maka akan terbentuk supermesh. Sumber arus dan komponen yang seri denganya dihilangkan, perhatikan gambar di bawah ini:

Gambar 5. Supermesh yang terbentuk
Terapkan KVL pada supermesh:
\(ΣV=0\)
\(-20+6i_1+10i_2+4i_2=0\)
\(6i_1+14i_2=20\)
dibagi 2
\(3i_1+7i_2=10\)……………………(1)
Terapkan KCL pada simpul dimana bertemu sumber arus dan arus mesh:
Perhatikan gambar di bawah ini:

Gambar 6. Simpul bertemunya sumber arus dan arus mesh
Berdasarkan gambit 6, kita dapat menerapkan KCL:
\(ΣI_{masuk}=ΣI_{keluar}\)
\(i_2=i_1+6\)……………..(2)
Menghitung arus mesh:
Persamaan (2) disubtitusi ke pers (1):
\(3i_1+7(i_1+6)=10\)
\(3i_1+7i_1+42=10\)
\(10i_1=-32\)
\(i_1=-3,2A\)……………………(3)
Subtitusikan pers (3) ke pers (2):
\(i_2=-3,2+6=2,8 A\)
Mencari arus sebenarnya:
Berdasarkan gambar pada soal, maka hubungan antara arus mesh dengan \(I_1, I_2\) dan \(I_3\):
\(I_1=i_1=-3,2 A\)
\(I_2=i_2=2,8 A\)
\(I_3\) searah dengan \(i_1\) dan berlawanan arah dengan \(i_2\) maka;
\(I_3=i_1-i_2\)
\(I_3=-3,2-2,8=-6 A\)