Dekoder atau Decoder adalah rangkaian kombinasi yang mengkonversi informasi biner dari n input menjadi maksimum \(2^n\) output. Jika ada yang tidak dipakai pada n input maka bagian ini disebut sebagai kondisi abai (don’t care) maka outputnya pasti lebih kecil dari \(2^n\). Misal terdapat 3 input maka total maksimal output yang dapat diperoleh adalah \( 2^3=8\).
Pada kesempatan ini, kita akan coba mempelajari 2-ke-4 garis dekoder atau bisa juga ditulis 2×4 dekoder, 2 menunjukkan banyaknya input, sedangkan 4 menunjukkan total kombinasi output yang diperoleh. Setiap output merepresentasikan satu sukumin dari 2 variabel inputnya. Perhatikan diagram blok berikut ini:
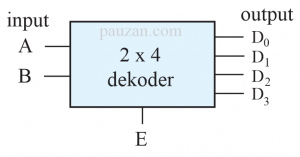
Gambar 1. Blok diagram dari 2×4 dekoder
Dari gambar 1 di atas, dapat disimpulkan bahwa dari 2 input dapat diperoleh maksimal \( 2^2=4\) output selain itu juga terdapat E yang berarti enable. Jika E=1 maka diagram blok dekoder dalam kondisi on, tapi jika E=0 maka dekoder menjadi off, tidak perduli seperti apa kondisi A maupun B. Artinya semua kombonasi output dari \(D_0,D_1,D_2\) dan \(D_3\) bernilai nol. Mari kita buat tabel kebenaran untuk 2×4 dekoder tersebut:
Tabel 1. Tabel kebenaran 2-ke-4 garis dekoder
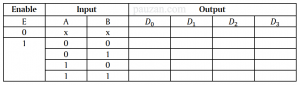
Berdasarkan gambar 1 di atas, pada input A dan B sama-sama x (kondisi don’t care) artinya mau berapapun nilai A dan B jika E=0 maka semua kombinasi outputnya bernilai nol, lihat tabel 2. Selanjutnya karena E=1 maka outputnya tergantung pada input A dan B. Kita coba untuk A=0 dan B=0, ingat input ini bernilai biner. Jadi pada B konversi nilai desimalnya adalah \(2^0\) dan A bernilai \(2^1\), B=0 maka \(2^0×0=0\), A=0 maka \(2^1×0=0\). Jadi nilai n adalah A+B=0+0=0, maka output yang hanya bernilai HIGH adalah \(D_0\) (berarti output untuk n=0), selain \(D_0\) bernilai LOW atau 0, tabel 1 di atas menjadi:
Tabel 2. Pengisian output \(D_0\)

Untuk input A=0 dan B=1, maka konversi ke desimalnya adalah B=1 maka \(2^0×1=1\), A=0 maka \(2^1×0=0\). Jadi nilai n adalah A+B=0+1=1. Jadi output yang bernilai HIGH hana output \(D_1\), begitu seterusnya sampai A=1 dan B=1, maka diperoleh \(2^0×1=1\) untuk B dan \(2^1×1=2\) untuk A. Sehingga n=2+1=3. Jadi output yang bernilai HIGH(1) adalah \(D_3\). Tabel 2 menjadi:
Tabel 3. Tabel kebenaran 2×4 dekoder
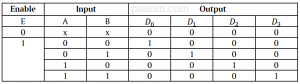
Berdasarkan tabel 3, persamaan Boolean untuk masing-masing output adalah:
\(D_0\): hanya bernilai 1 untuk A=0, B=0 maka persamaannya menjadi \(D_0=A’B’\).
\( D_1\): hanya bernilai 1 saat A=0, B=1 maka persamaannya menjadi \(D_1=A’B\)
\(D_2\): hanya bernilai 1 saat A=1, B=0 maka persamaannya menjadi \(D_2=AB’\)
\(D_3\): hanya bernilai 1 saat A=1, B=1 maka persamaannya menjadi \(D_3=AB\)
Note: disajikan dalam bentuk sukumin maka jika bernilai 0 dikomplemen jika 1 tidak dikomplemen.
Setelah persamaannya diperoleh, kita selanjutnya membuat rangkaiannya menggunakan gerbang AND dan inverter. Perhatikan gambar berikut:
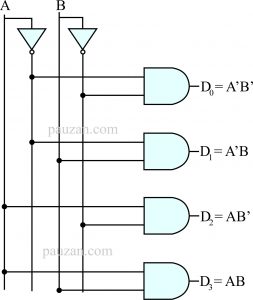
Gambar 2. Rangkaian untuk 2×4 dekoder
Untuk menguji apakah rangkaian di atas sama hasilnya dengan tabel kebenaran pada tabel 3, silahkan menggunakan software Pspice.