Fungsi singularitas merupakan fungsi yang memilki sifat diskontinuitas. Dalam menganalsis rangkaian ada tiga fungsi singularitas yang sangat penting untuk dipahami yaitu fungsi step, impuls dan fungsi ramp.
Fungsi step
Lambang dari fungsi ini adalah \( u(t) \), fungsi step bernilai 0 untuk nilai negatif t (waktu) dan 1 untuk nilai positif dari t. Secara matematis dapat dituliskan sebagai berikut:
\(u(t)=\left\{\begin{matrix} 0, & t<0\\ 1, & t>0 \end{matrix}\right.\)………(1)
Pada saat t=0, fungsi step tak terdefinisi dimana pada saat itu terjadi perubahan secara cepat dari 0 ke 1. Fungsi step tak berdimensi separti halnya fungsi trigonometri. Jika digambar bentuk fungsinya, maka dapat dilihat pada gambar berikut ini:
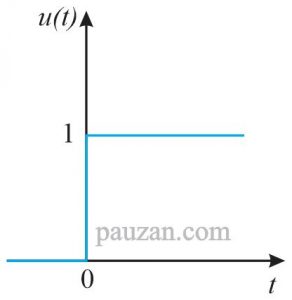
Gambar 1. Fungsi step
Jika perubahan keadaan dari 0 ke 1 terjadi saat \( t=t_0 \) seperti pada gambar berikut ini:
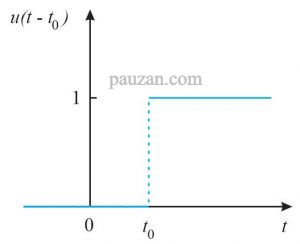
Gambar 2. Fungsi step lebih lambat sebesar \( t_0 \)
maka berdasarkan gambar 2 di atas, perubahan nilai dari 0 ke 1 tidak terjadi pada titik 0 melainkan terjadi setelah selang waktu \( t_0 \), kondisi ini disebut fungsi step lebih lambat sebesar \( t_0 \). Persamaan fungsi step menjadi:
\(u(t-t_0)=\left\{\begin{matrix} 0, & t<t_0\\ 1, & t>t_0 \end{matrix}\right.\)…………….(2)
Berikutnya jika fungsi step berbentuk seperti pada gambar di bawah ini:
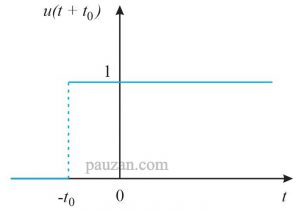
Gambar 3. Fungsi step lebih cepat sebesar \( t_0 \)
maka berdasarkan gambar 3, terjadi perubahan dari 0 ke 1 pada saat \( -t_0 \) dan ini terjadi sebelum titik 0 maka kondisi ini menyebabkan fungsi step terjadi lebih cepat sebesar \( -t_0 \). Persamaan fungsi stepnya menjadi:
\(u(t+t_0)=\left\{\begin{matrix} 0, & t<-t_0\\ 1, & t>-t_0 \end{matrix}\right.\)……………..(3)
Fungsi step digunakan untuk merepresentasikan perubahan cepat dari tegangan atau arus. Sebagai contoh, suatu tegangan memiliki persamaan sebagai berikut:
\(v(t)=\left\{\begin{matrix} 0, & t<t_0\\ V_0, & t>t_0 \end{matrix}\right.\)……………(4)
Sekarang kita coba \( V_0 \)dikali dengan fungsi step \( u(t-t_0) \), maka:
\(V_0u(t-t_0)=V_0\left\{\begin{matrix} 0, & t<t_0\\ 1, & t>t_0 \end{matrix}\right.\)\(V_0u(t-t_0)=\left\{\begin{matrix} 0 . V_0, & t<t_0\\ 1.V_0, & t>t_0 \end{matrix}\right.\)
\(V_0u(t-t_0)=\left\{\begin{matrix} 0, & t<t_0\\ V_0, & t>t_0 \end{matrix}\right.\)……(5)
Persamaan (5) sama dengan persamaan (4) di atas maka tegangan juga dapat ditulis:
\( v(t)=V_0u(t-t_0) \)………………………..(6)
Jika \( t_0=0 \)maka persamaan (6) menjadi \( v(t)=V_0 u(t) \), sumber tegangan \( V_0 u(t) \)dapat dilihat pada gambar 4a sedangkan rangkaian eqivalen (yang setara) dengannya dapat dilihat pada gambar 4b:
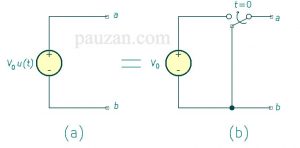
Gambar 4 (a) sumber tegangan \( V_0 u(t) \)dan (b) rangkaian eqivalennya
Berdasarkan gambar 4b di atas, saat t<0 terminal a-b terhubung pendek (short circuit) maka tegangannya adalah v=0 sedangkan saat t>1 sakelar berpindah ke atas, terminal a-b terhubung dengan sumber tegangan, maka tegangan pada saat tersebut adalah \( v=V_0 \).
Dengan cara yang sama, sumber arus \( I_0 u(t) \)dapat dilihat pada gambar 5a dan rangkaian eqivalennya pada gambar 5b di bawah ini:
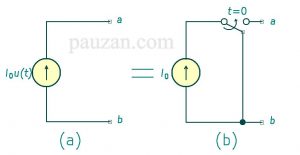
Gambar 5 (a) sumber arus \( I_0 u(t) \)dan (b) rangkaain eqivalennya
Perhatikan bahwa untuk sumber arus, saat t<0 terminal a-b menjadi rangkaian terbuka (open circuit) maka arus yang mengalir diantara terminal a-b adalah i=0, sedangkan saat t>0 terminal a-b terhubung sumber arus, maka arus yang mengalir sebesar \( i=I_0 \).
Fungsi impuls (delta)
Turunan fungsi step adalah fungsi impuls, lambangnya \( δ(t) \)yang ditulis sebagai:
\( \delta (t)=\frac{d}{dt}u(t)\)……………………………………(7)
Maka persamaan (1) diturunkan terhadap waktu adalah:
\(\delta (t)=\left\{\begin{matrix} 0, & t<0 \\ tak terdefinisi, & t=0 \\ 1, & t>0 \end{matrix}\right.\)……………………..(8)
Berdasarkan persamaan (8) di atas, dapat disimpulkan bahwa fungsi impuls (disebut juga sebagai fungsi delta) bernilai 0 dimanapun kecuali di t=0 bernilai tak terdefinisi. Fungsi impuls divisualisasikan untuk durasi pulsa yang sangat pendek pada satuan luas, sehingga dapat diekspresikan dalam bentuk integral:
\( \int_{0-}^{0+}\delta (t)dt=1 \)………………………(9)
0- berarti sesaat sebelum t=0 dan 0+ berarti sesaat setelahnya. Satuan luas disebut juga sebagai ketinggian fungsi impuls. Sebagai contoh suatu fungsi impuls 10δ(t) memiliki luas 10 (ketinggian 10), sedangkan 5δ(t+2) berarti memiliki luas 5 (ketinggiannya 5) dan lebih cepat 2 sekon dari t=0. Begitu juga dengan -4δ(t-3), ketinggiannya -4 dan lebih lambat 3 sekon dari t=0. Perhatikan gambar berikut ini:
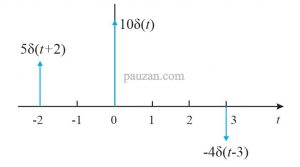
Gambar 6. Tiga fungsi impuls
Apakah bisa fungsi impuls mempengaruhi fungsi yang lain? untuk menjawabnya mari perhatikan integral berikut ini:
\( \int_a^b f(t)\delta (t-t_0)dt \)…………………………….(10)
dimana a<t_0<b. Ingat \( δ(t-t_0 )=0 \)kecuali pada \( t=t_0 \)bernilai tak terdefinisi.
Berdasarkan persamaan (2) dan (8) dapat disimpulkan:
\( δ(t-t_0 )=0 \)untuk a karena \( a<t_0 \), maka persamaan (10) menjadi;
\( f(a)δ(a-t_0 )=f(a). 0=0 \)Berdasarkan persamaan (9), \( δ(t-t_0 )=1\) untuk \( t=t_0 \), maka persamaan (10) menjadi;
\( f(t_0 )δ(t-t_0 )=f(t_0 ).1=f(t_0) \)\( δ(t-t_0 )=0 \)untuk b karena b>0, maka;
\( f(b)δ(t-t_0 )=f(b). 0=0 \)Jadi persamaan (10) menghasilkan:
\( \int_a^b f(t) \delta (t-t_0)dt=f(t_0) \)………………………(11)
Berdasarkan persamaan (11) dapat disimpulkan bahwa jika suatu fungsi diintegralkan dengan fungsi impuls maka diperoleh fungsi itu pada titik dimana terjadi impuls.
Jika pada persamaan (11) \( t_0=0 \)maka;
\( \int_{0-}^{0+}f(t) \delta (t)dt=f(0) \)………………………..(12)
Fungsi Ramp
Jika pada pembahasan sebelumnya turunan fungsi step menghasilkan fungsi impuls, maka jika fungsi step diintegralkan menghasilkan fungsi ramp, lambangnya \( r(t) \). Secara matematis ditulis:
\( r(t)=\int_{-\infty}^{t}u(t)dt=tu(t) \)………………….(13)
Mengacu ke persamaan (1), maka;
t≤0, misal t=-2
\( tu(t)=-2 u(-2) \) \( r(t≤0)=-2 . 0=0 \)Berapapun nilai t jika bernilai negatif akan menghasilkan fungsi ramp dengan nilai 0. Sekarang kita coba untuk t positif:
t≥0, misal t=1
\( tu(t)=1 u(1) \) \( r(1)=1 . 1=1 \)Jika t=3
\( tu(t)=3 u(3) \) \( r(3)=3 . 1=3 \)Perhatikan bahwa jika t positif maka fungsi ramp bernilai t itu sendiri, jadi persamaan (13) dapat juga ditulis:
\(r(t)=\left\{\begin{matrix} 0, &t\leq 0 \\ t, &t\geq 0 \end{matrix}\right.\)………….(14)
Fungsi ramp adalah fungsi yang bernilai 0 untuk t negatif dan memiliki slope (gradient) untuk t positif. Perhatikan gambar berikut ini yang merupakan grafik untuk fungsi ramp.
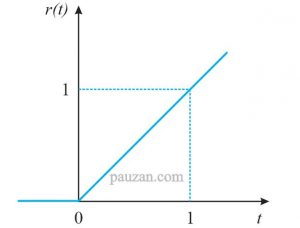
Gambar 7. Fungsi ramp
Fungsi ramp bisa juga diperlambat dan dipercepat, untuk fungsi yang diperlambat sebesar \( t_0 \)dapat dilihat grafikanya pada gambar berikut ini:
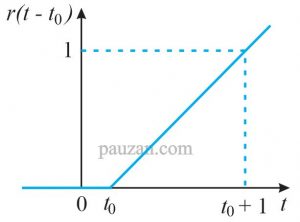
Gambar 8. Fungsi ramp yang diperlambat
Berdasarkan gambar 8, maka persamaan fungsi rampnya adalah:
\(r(t-t_0)=\left\{\begin{matrix} 0, &t\leq t_0 \\ t-t_0, &t\geq t_0 \end{matrix}\right.\)……..(15)
Fungsi ramp yang dipercepat dapat dilihat pada gambar berikut ini:
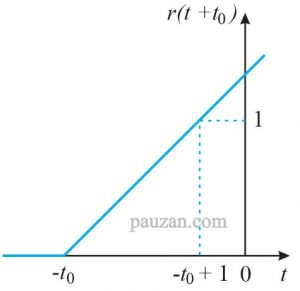
Gambar 9. Fungsi ramp yang dipercepat
Berdasarkan gambar 9, fungsi rampnya adalah:
\(r(t+t_0)=\left\{\begin{matrix} 0, &t\leq -t_0 \\ t+t_0, &t\geq -t_0 \end{matrix}\right.\)…..(16)
Hubungan antara ketiga fungsi singularitas
Ketiga fungsi singular yaitu fungsi step, impuls dan ramp, hubungan ketiganya dapat diperoleh melalui turunan dan integral.
Hubungan menggunakan turunan
\( \delta (t)=\frac{du(t)}{dt} \)\( u(t)=frac{dr(t)}{dt} \)
Hubungan menggunakan integral:
\( u(t)=\int_{-\infty}^{t} \delta (t)dt \)
\( r(t)=\int_{-\infty}^{t} u(t)dt \)
Contoh Soal 1
Ekspresikan pulsa tegangan berikut ke dalam bentuk fungsi step, lalu hitunglah derivative dan gambarlah fungsi hasil penurunannya.
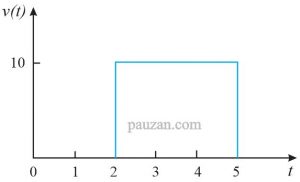
Gambar 10. Soal fungsi singularitas
Jawab
Berdasarkan gambar di atas, bentuknya disebut sebagai fungsi gate, fungsi ini ditandai dengan fungsi step yang bernilai 0 pada t tertentu dan 1 pada t yang lain. Berdasarkan gambar, fungsi step mulai bernilai 1 dari t=2 dan ke 0 lagi pada t=5. Maka dari keadaan ini dapat disimpulkan bahwa fungsi di atas terdiri dari dua fungsi step seperti terlihat pada gambar berikut ini:
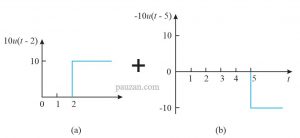
Gambar 11. Dekomposisi dari pulsa tegangan (a) perubahan dari 0 ke 1 pada t=2 (b) perubahan dari 1 ke 0 pada t=5
Berdasarkan gambar 11, maka fungsi stepnya adalah:
\( v_1=10u(t-2) \)
\( v_2=-10u(t-5) \)
Penjumlahan kedua fungsinya adalah sebagai berikut:
\( v(t)=v_1+v_2 \)
\( v(t)=10u(t-2)-10u(t-5) \)
\( v(t)=10[u(t-2)-u(t-5)] \)
Berikutnya dilakukan penurunan terhadap fungsi step yang diperoleh, maka hasilnya berupa fungsi impulse:
\( \frac{dv}{dt}=10[\frac{du(t-2)}{dt}-\frac{du(t-5)}{dt}] \)\( \frac{dv}{dt}=10[\delta (t-2)-\delta(t-5)] \)
Selanjutnya membuat grafik fungsi impuls di atas:
Terdapat dua impuls, 10δ(t-2) dan -10δ(t-5).
10δ(t-2)= ketinggian impulsnya 10 dan terjadi pada t=2
-10δ(t-5)= ketinggiannya -10 dan impulsnya terjadi pada t=5.
Berikut ini adalah gambar hasil dari derivatifnya:
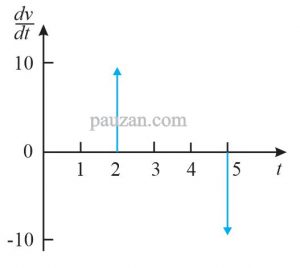
Gambar 12. Penurunan dari tegangan
Contoh soal 2
Ekspresikan fungsi sawtooth berikut ini ke bentuk fungsi singularitas.
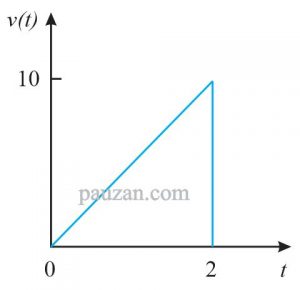
Gambar 13. Soal fungsi singularitas
Jawab
Berdasarkan gambar 13, bentuk pulsanya adalah penggabungan antara fungsi ramp (adanya slope) dan fungsi step (setelah t=2, v(t) bernilai 0). Jadi persamaan fungsi untuk gambar 13 di atas adalah:
\( v(t)=v_1 (t)+v_2 (t)+v_3 (t) \)
Menghitung \( v_1 \)
\( v_1 \)adalah dari t=0 sampai dengan t=2, ini berbentuk fungsi ramp. Perhatikan gambar berikut ini:
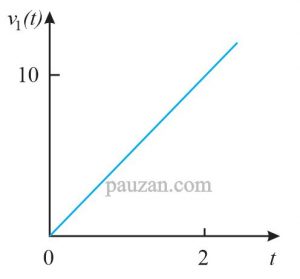
Gambar 14. Gelombang sawtooth dipecah-pecah
Berdasarkan gambar 14, fungsi rampnya adalah:
\( v_1 (t)=5r(t) \)
Menghitung \( v_2 \)
Berdasarkan gambar 14, slopenya akan terus naik sampai takhingga. Untuk mengatasi ini, dibuatlah bentuk slope yang sama besar tapi berlawanan arah supaya jika dijumlahkan maka akan menghasilkan kurva yang stagnan. Perhatikan gambar untuk \( v_2 \):
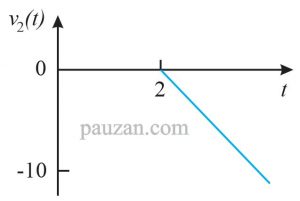
Gambar 15. Dekomposisi gelombang sawtooth
Berdasarkan gambar 15, persamaan fungsi rampnya adalah:
\( v_2 (t)=-5r(t-2) \)
Jika bentuk gelombang \( v_1 \)dan \( v_2 \)dijumlahkan, maka hasilnya adalah:
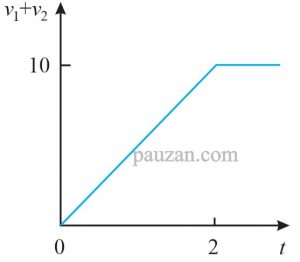
Gambar 16. Hasil penjumlahan \( v_1 \)dengan \( v_2 \)
Menghitung \( v_3 \)
Supaya bentuk gelombangnya turun pada t=2 maka dibuat \( v_3 \)yang merupakan fungsi step. Perhatikan bentuk gelombangnya:
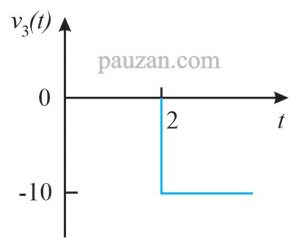
Gambar 17. Bentuk fungsi step
Berdasarkan gambar 17, fungsi stepnya adalah:
\( v_3 (t)=-10u(t-2) \)
Selanjutnya adalah menjumlahkan ketiga fungsi singularitas yang sudah diperoleh:
\( v(t)=5r(t)-5r(t-2)-10u(t-2) \)
Sehingga penjumlahannya menghasilkan:
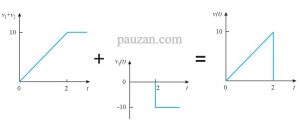
Gambar 18. Pulsa yang dihasilkan dari fungsi singularitas.
NEXT: Respon Step Rangkaian RC