Pada pembahasan sebelumnya, kita sudah mendapatkan persamaan tegangan-arus dalam bentuk fasor untuk tiga elemen pasif (resistor, induktor dan kapasitor). Berikut persamaan masing-masing elemen:
Resistor:
\( \vec{V}=R \vec{I} \)………………………………………………………(1)
Induktor:
\( \vec{V}=j\omega L \vec{I} \)…………………………………………………………(2)
Kapasitor:
\( \vec{V}=\frac{\vec{I} }{j\omega C} \)…………………………………………….(3)
Impedansi
Impedansi adalah perbandingan antara tegangan fasor \( V \) dengan arus fasor \( I \), satuannya adalah ohm (\( Ω \)):
\( \vec{Z}=\frac{V}{I} \)………………………………………………….(4)
Ingat meskipun impedansi adalah hasil pembagian dua fasor, tapi impedansi bukanlah fasor karena impedansi bukanlah suatu sinusoid yang berubah-ubah amplitudonya berdasarkan waktu. Berdasarkan persamaan (4), kita bisa menulis impedansi untuk tiap-tiap elemen:
Resistor:
\( \frac{\vec{V} }{\vec{I} }=R \)……………………………………………..(5)
Induktor:
\( \frac{\vec{V} }{\vec{I}}=\vec{Z_L}=j\omega L \)………………………………………(6)
Kapasitor:
\( \frac{\vec{V} }{\vec{I} }=\vec{Z_C}=\frac{1}{j\omega C} \)………………………(7)
Secara umum impedansi dapat ditulis dalam bentuk kartesian, seperti di bawah ini:
\( \vec{Z}=R+jX \)……………………………………………..(8)
\( R \) adalah resistansi, sedangkan \( \vec{X} \) adalah reaktansi.
Jika dalam suatu rangkaian yang terdapat hanya dua elemen pasif: resistor dan induktor maka persamaan (8) dapat ditulis:
\( \vec{Z}=R+\vec{Z_L} \)………………………………………….(9)
Jika kita subtitusikan persamaan (6) maka diperoleh:
\( \vec{Z}=R+j\omega L \)
Persamaan di atas disebut sebagai impedansi induktif.
Jika dalam rangkaian hanya ada dua elemen: resistor dan kapasitor maka impedansinya adalah:
\( \vec{Z}=R+\vec{Z_C} \)
Maka;
\( \vec{Z}=R+\frac{1}{j\omega C} \)…………………………………….(10)
Impedansi juga dapat ditulis dalam bentuk polar:
\( \vec{Z}=|\vec{Z}|\angle \theta \)……………………………………….(11)
Dimana:
\( |\vec{Z}|=\sqrt{R^2+X^2} \)…………………………………………….(12)
Dan
\( \theta =\tan^{-1} \frac{X}{R} \)…………………………………………..(13)
\( R=|\vec{Z}|\cos \theta \)………………………………………………….(14)
\( X=|\vec{Z} |\sin \theta \)…………………………………………………..(15)
Admitansi
Admitansi adalah resiprok dari impedansi, artinya angka satu dibagi dengan impedansi, satuannya adalah siemens(S):
\( \vec{Y}=\frac{1}{\vec{Z} }=\frac{\vec{I}}{\vec{V}} \)………………………….(16)
Persamaan di atas juga dapat ditulis:
\( \vec{Y}=G+jB \)……………………………………………………………………(17)
Dimana \( G \) adalah konduktansi dan \( B \) adalah suspektansi. Berapakah nilai \( G \) dan \( B \)? Dengan membandingkan persamaan (8) dengan (17) maka;
\( G+jB=\frac{1}{R+jX} \)
Dikalikan dengan akar sekawan:
\( =\frac{1}{R+jX} \frac{R-jX}{R-jX}=\frac{R-jX}{R^2+X^2} \)
Maka;
\( G+jB=\frac{R}{R^2+X^2 }+\frac{-jX}{R^2+X^2} \)
Dengan membagi antara riil dan imajiner maka:
\( G=\frac{R}{R^2+X^2}\)………………………………………………..(18)
\( B=\frac{-X}{R^2+X^2}\)………………………………………………..(19)
Contoh Soal
Tentukan \( v(t) \) dan \( i(t) \) pada rangkaian di bawah ini:
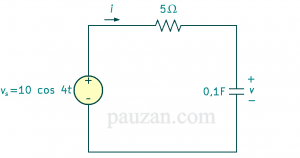
Gambar 1. Soal impedansi pada rangkaian AC
Jawab
Rubah tegangan ke fasor:
\( v_s=10 \cos 4t \)
Maka:
\( V_m=10 \)\( \omega=4 \)
\( \phi=0^{o} \)
Bentuk fasornya:
\(\vec{V_s}=V_m \angle \phi \)\(\vec{V_s}=10 \angle 0^{o} \)
Menghitung impedansi:
Kita gunakan persamaan (10):
\(\vec{Z}=R+\frac{1}{j \omega C} \)\(\vec{Z}=5+\frac{1}{j\times 4\times 0,1}=5+\frac{1}{j0,4} \)
Pada pembahasan fasor, diperoleh:
\( \frac{1}{j}=-j \)
Maka;
\( \vec{Z} =5-j(\frac{1}{0,4})=5-j2,5 \Omega \)
Menghitung arus:
\( I=\frac{V_s}{Z}=\frac{10∠0^{o}}{5-j2,5} \)
Karena pembagian, maka dirubah ke bentuk polar. Jadi penyebutnya menjadi:
\( 5-j2,5=I_m\angle \phi \)\( I_m=\sqrt{x^2+y^2}=\sqrt{25+6,25} \)
\( I_m=5,59 \)
\( \phi =\tan^{-1}\frac{y}{x}=\tan^{-1}\frac{-2,5}{5} \)
\( \phi=-26,56^{o} \)
Maka;
\( 5-j2,5=5,59 \angle (-26,56^{o}) \)
Jadi arusnya adalah:
\( \vec{I}=\frac{10\angle 0^{o}}{5,59 \angle (-26,56^{o})} \)\( \vec{I}=\frac{10}{5,59} \angle 0^{o}-(-26,56^{o}) \)
\( \vec{I}=1,79 \angle 26,56^{o} \)
Bentuk sinusoidnya:
\( i(t)=1,79 \cos (4t+26,56^{o}) \) A
Menghitung tegangan pada kapasitor
Tegangan pada kapsitor adalah:
\( v=iz_C \)
Dimana \( z_c \) adalah impedansi dari kapasitor, kita sudah mendapatkan \( i \) dan fasornya. Tegangan fasor pada kapasitor adalah:
\( \vec{V}=\vec{I} \vec{Z_C} \)\( \vec{V}=[1,79 \angle 26,56^{o}] \times \frac{1}{j\omega C} \)
\( \vec{V}=\frac{1,79 \angle 26,56^{o}}{j\times 4 \times 0,1}=\frac{1,79 \angle 26,56^{o}}{j0,4} \)
Karena berbentuk pembagian maka pembilang dan penyebut diubah ke bentuk polar, pembilang sudah pada bentuk polar, maka tinggal merubah penyebutnya:
\( j0,4=0+j0,4 \)
Mencari \( r \);
\( r=\sqrt{x^2+y^2}=\sqrt{0^2+(0,4)^2} \)\( r=0,4 \)
Mencari \( \phi \);
\( \phi =\tan^{-1}\frac{y}{x}=\tan^{-1}\frac{0,4}{0} \)\( \phi =\tan^{-1}(\infty)=90^{o} \)
Jadi:
\( j0,4=0,4 \angle 90^{o} \)
Persamaan \( \vec{V} \) menjadi;
\( \vec{V}=\frac{1,79\angle 26,56^{o}}{0,4 \angle 90^{o}}=\frac{1,79}{0,4}\angle 26,56^{o}-90^{o} \)
\( \vec{V}=4,475 \angle (-63,44^{o}) \) V
Diubah ke bentuk sinusoid:
\( v(t)=4,475 \cos (4t-63,44^{o}) \) V
Coba kita bandingkan arus dan tegangan:
\( i(t)=1,79 \cos (4t+26,56^{o}) \) A
Tegangannya kita buat menjadi:
\( v(t)=4,475 \cos (4t+26,56^{o}-90^{o}) \) V
\( v(t) \) tertinggal (karena tanda negatif) sebesar \( 90^{o} \) dari arus \( i(t) \).
PREVIOUS: Persamaan fasor pada R, L dan C
NEXT: Kombinasi impedansi