Induktor dirangkai seri
Perhatikan rangkaian induktor berikut;
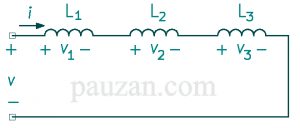
Gambar 5. Induktor dirangkai seri
Berdasarkan gambar di atas, arus yang melalui induktor pertama sampai terakhir adalah sama, dengan menerapkan hukum tegangan Kirchhoff (KVL);
\(v=v_1+v_2+v_3\)……………………………………………….(8)
Berdasarkan persamaan (1) di atas,\(v=L\frac{di}{dt}\) maka;
\(v=L_1\frac{di}{dt}+ L_2\frac{di}{dt} + L_3\frac{di}{dt}\)\(v=(L_1+L_2+L_3)\frac{di}{dt}\)
\(v=L_{eq}\frac{di}{dt}\)………………………………………….(9)
Dimana \(L_{eq}\) adalah;
\(L_{eq}=L_1+L_2+L_3\)……………………………………………..(10)
Jadi induktansi dari induktor yang dihubung seri sama halnya dengan resistor yang dihubung seri yaitu dijumlahkan.
Induktor yang dirangkai paralel
Perhatikan rangkaian berikut;
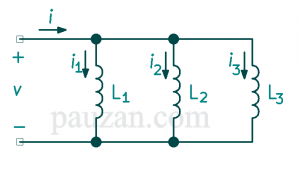
Gambar 6. Induktor yang disusun paralel
Berdasarkan gambar di atas, jumlah arus yang melalui tiap induktor adalah arus total ;
\(i=i_1+i_2+i_3\)……………………………………….(11)
Dari persamaan (5) persamaan di atas menjadi;
\(i=\frac{1}{L} \int_{t_0}^{t} v(t) dt+i(t_0)\);
\(i=\frac{1}{L_1} \int_{t_0}^{t} v(t) dt+i_1(t_0)+ \frac{1}{L_2} \int_{t_0}^{t} v(t) dt+i_2(t_0)+ \frac{1}{L_3} \int_{t_0}^{t} v(t) dt+i_3(t_0)\)Jadi;
\(i=(\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3})\int_{t_0}^{t}vdt+i_1(t_0)+ i_2(t_0)+ i_3(t_0)\)Persamaan di atas dapat ditulis sebagai;
\(i=\frac{1}{L_eq}\int_{t_0}^{t}vdt+i(t_0)\)………………………(12)
Dimana;
\(\frac{1}{L_eq}=\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{L_3}\)…………………….(13)
dan
\(i(t_0)=i_1(t_0)+ i_2(t_0)+ i_3(t_0)\)………………………(14)
Jika terdapat empat induktor disusun paralel maka cukup dengan menambahkan pada persamaan (13), begitu seterusnya.
Contoh Soal 1
Perhatikan gambar di bawah ini:
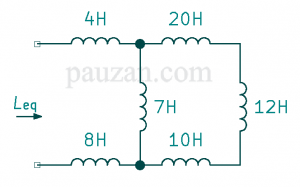
Gambar 7. Soal induktor rangkai seri-paralel
Tentukanlah induktansi eqivalen dari rangkaian di atas.
Jawab
Induktor 20 H, 12 H dan 10 H tersusun seri artinya induktansi serinya dapat dicari dengan menjumlahkan ketiganya:
\(L_s=20+12+10=42 H\)Rangkaiannya menjadi;
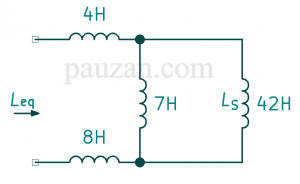
Gambar 8. Rangkaian setelah diperoleh \(L_s\)
Induktansi seri \(L_s\) sekarang paralel dengan 7 H, maka induktansi paralelnya;
\(\frac{1}{L_p}=\frac{1}{7}+\frac{1}{42}\);
\( \frac{1}{L_p}=\frac{6+1}{42}=\frac{7}{42}\);
\(L_p=6 H\)Rangkaiannya menjadi seperti gambar di bawah ini;
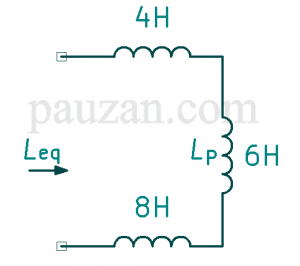
Gambar 9. Rangkaian setelah diparalel antara \(L_s\) dengan 7 H
Karena yang tertinggal hanya rangkaian seri maka induktansi eqivalennya adalah;
\(L_{eq}=4+6+8=18 H\)
Contoh Soal 2
Perhatikan rangkaian berikut ini:
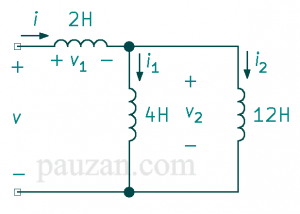
Gambar 10. Contoh soal 2
Arus yang mengalir pada rangkaian di atas adalah;
\(i(t)=4(2-e^{-10t})\) mA
Jika \(i_2(0)=-1\) mA, tentukan;
a. \(i_1(0)\)
b.\(v(t), v_1(t), v_2(t)\)
c.\(i_1(t), i_2(t)\)
Jawab
a. Berdasarkan gambar pada soal, arus \(i_1(0)\) adalah pengurangan arus total pada detik ke-0 oleh arus pada induktor 2 pada detik ke-0;
\(i_1(0)=i(0)-i_2(0)\)Mencari \(i(0)\)
Berdasarkan persamaan arus pada soal;
\(i(t)=4(2-e^{-10t})\) mA
\(i(0)=4(2-e^{-0})=4(2-1)=4\) mA.
Sedangkan \(i_2(0)\) sudah diketahui dari soal, maka arus \(i_1(0)\) menjadi;
\(i_1(0)=4-(-1)=5\) mA.
b. Mencari tegangan
Tegangan dapat dicari melalui persamaan (9), terlebih dahulu kita cari induktansi eqivalen dari rangakaian di atas;
Induktor 4 H dan 12 H paralel maka induktansi dari keduanya;
\(\frac{1}{L_p}=\frac{1}{4}+\frac{1}{12}=\frac{3+1}{12}=\frac{4}{12}\)\(L_p=3\) H
Sekarang \(L_p\) tersusun seri dengan 2 H maka \(L_{eq}\) adalah;
\(L_{eq}=2+3=5\) H
Sehingga persamaan tegangan induktor \(v(t)\) pada rangakaian di atas menjadi;
\(v(t)=L_{eq}\frac{di}{dt}=5\frac{d}{dt}4(2-e^{-10t})\) \(v(t)=5\frac{d}{dt}(8-4e^{-10t})\)Turunan 8 terhadap waktu adalah 0 maka;
\(v(t)=5(0-\frac{d}{dt}(-4e^{-10t})=-5\frac{d}{dt}(4e^{-10t})\)\(v(t)=-5 . 4 . (-10)e^{-10t}=200e^{-10t}\) mV
dan
\(v_1(t)=2\frac{di}{dt}=2\frac{d}{dt}(4(2-e^{-10t}))=2(-4)(-10)e^{-10t}\)\(v_1(t)=80e^{-10t}\) mV
Karena \(v=v_1+v_2\) maka;
\(v_2=v-v_1=200e^{-10t}-80e^{-10t}\)\(v_2(t)=120e^{-10t}\) mV
c. Menghitung arus
Persamaan yang digunakan adalah persamaan 12:
\(i=\frac{1}{L_{eq}}\int_{t_0}^{t}vdt+i(t_0)\)Persamaannya menjadi;
\(i_1(t)=\frac{1}{L_{i_1}}\int_{t_0}^{t}v_2dt+i(0)\)\(L_{i_1}\) adalah induktansi 4 H sedangkan \(v_2\) adalah tegangan pada 4 H, maka;
\(i_1(t)=\frac{1}{4}\int_{t_0}^{t}120e^{-10t}dt+5\) mA
\(i_1(t)=\frac{120}{4}\int_{t_0}^{t}e^{-10t}dt+5mA=30. \frac{1}{-10}(e^{-10t}-e^0) +5 mA\)\(i_1(t)=-3e^{-10t}+3+5=8-3e^{-10t}\) mA
Dengan cara yang sama,
\(i_2(t)=e^{-10t}\) mA.
PREVIOUS: Induktor