Kapasitor dirangkai Paralel
Kapasitor yang dirangkai paralel ditunjukkan seperti pada gambar berikut:
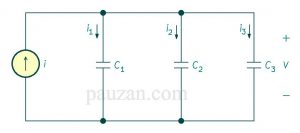
Gambar 8. Kapasitor dirangkai paralel
Perhatikan bahwa pada rangkaian di atas, arus tiap kapasitor berbeda. Persamaan kapasitansi ekuivalennya adalah sebagai berikut:
\( C_{eq}=C_1+C_2+C_3 \)……………………………………….(8)
Jadi persamaan kapasitansi eqivalen ini berbanding terbalik dengan persamaan resistansi pada resistor.
Kapasitor dirangkai Seri
Rangkaian seri dari kapsitor dapat dilihat pada gambar di bawah ini:
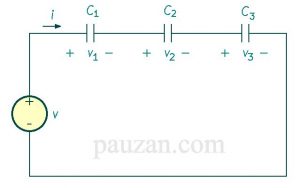
Gambar 9. Kapasitor disusun seri
Untuk kapasitor yang disusun seri, arusnya sama (untuk kasus AC) tapi tegangannya berbeda-beda. Sedangkan persamaan kapasitansi ekuivalennya adalah:
\( \frac{1}{C_{eq}} =\frac{1}{C_1} +\frac{1}{C_2} +\frac{1}{C_3} \)…………………(9)
Contoh Soal 1
Tentukanlah kapasitansi ekuivalen antara terminal a dan b pada rangkaian berikut ini:
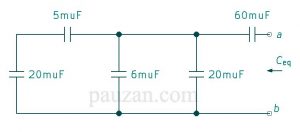
Gambar 10. Soal rangkaian seri-paralel kapasitor
Jawab
5μF dan 20μF seri maka;
\( \frac{1}{C_{s1}} =\frac{1}{5μ}+\frac{1}{20μ}=\frac{4+1}{20μ}=\frac{5}{20μ} \)\( C_{s1}=4μF \)
Rangkaiannya menjadi;
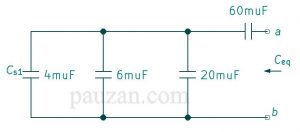
Gambar 11. Rangkaian setelah diperoleh \( C_{s1} \)
Sekarang \( C_{s1} \) paralel dengan \( 6μF \) maka;
\( C_{p1}=C_{s1}+6μF=4μF+6μF=10μF \)Rangkaiannya menjadi;
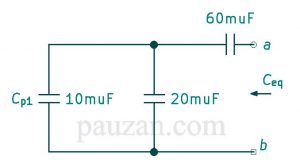
Gambar 12. Rangkaian setelah diperoleh \( C_{p1} \)
Seanjutnya \( C_{p1} \) paralel dengan \( 20μF \)maka;
\( C_{p2}=10μF+20μF=30μF \)Rangkaiannya menjadi;
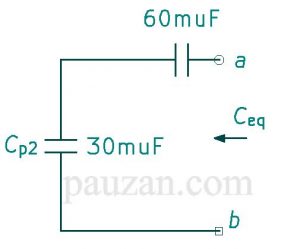
Gambar 13. Rangkaian setelah diperoleh \( C_{p2} \)
Sekarang \( C_{p2} \) seri dengan \( 60μF \) maka kapasitansi eqivalennya adalah;
\( \frac{1}{C_{eq}} =\frac{1}{30μ}+\frac{1}{60μ}=\frac{2+1}{60μ}=\frac{3}{60μ} \)\( C_{eq}=20 \) μF
Contoh Soal 2
Perhatikan gambar berikut:
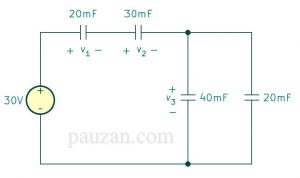
Gambar 14. Kapasitor yang diberi sumber tegangan DC
Tentukanlah tegangan pada tiap kapasitor
Jawab
Pertama kita akan mencari kapasitansi ekuivalen dari rangkaian sehingga kita dapat memperoleh total muatan pada rangkaian tersebut. 20 mF dan 30 mF tersusun seri maka kapasitansinya adalah;
\( \frac{1}{C_s} =\frac{1}{20}+\frac{1}{30}=\frac{3+2}{60}=\frac{5}{60} \)
\( C_s=12 \) mF
Rangkaiannya menjadi:
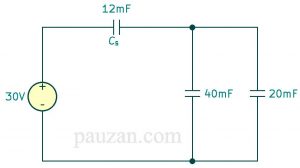
Gambar 15. Rangkaian setelah diseri antara 20mF dengan 30mF
Sekarang kita paralelkan antara 20mF dengan 40mF;
\( C_p=20+40=60 \) mF
Rangkaiannya menjadi;
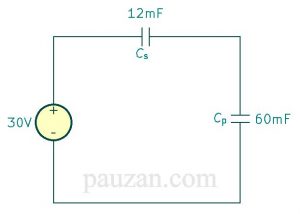
Gambar 16. Setelah 20mF dan 40mF diparalelkan
Terakhir, kita seri antar \( C_s \)dengan \( C_p \) ;
\( \frac{1}{C_{eq}} =\frac{1}{12}+\frac{1}{60}=\frac{5+1}{60} \)
\( C_{eq}=10 \) mF
Jadi rangkaiannya menjadi;
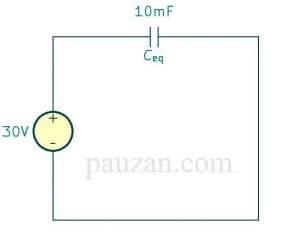
Gambar 17. Rangkaian setara \( C_{eq} \)
Oleh karena itu muatan pada rangkain sebesar;
\( q=C_{eq} V=10 mF . 30 volt=0,3 \)C
Kembali perhatikan gambar 14, bahwa kapasitor 20 mF dan 30 mF tersusun seri dengan 30 V, artinya muatan pada kapasitor tersebut sama dengan muatan ekuivalen 0,3 C.
NOTE: Supaya mudah memahami konsep muatan, analogikan saja dengan arus. Jika pada rangkaian seri maka muatannya sama tapi kalau dalam rangkaian paralel maka muatannya terbagi.
Tegangan pada kapasitor tersebut adalah;
\( v_1=\frac{q}{C_1} =\frac{0,3}{20\times10^{-3}}=15 \) V
\( v_2=\frac{q}{C_2} =\frac{0,3}{(30\times10^{-3}}=10 \) V
Berapakah muatan pada kapasitor paralel 40 mF dan 20 mF? Karena paralel maka tegangannya sama. Artinya tegangannya diperoleh dengan cara mengurangi tegangan sumber (30V) dengan tegangan pada kapasitor 20 mF dan 30 mF;
\( v_3=30-15-10=5 \) V
Jadi tegangan pada kapasitor 20 mF dan 40 mF masing-masing 5 V.