Fasor adalah bilangan kompleks yang merepresentasikan amplitudo dan fasa dari suatu sinusoidal. Rangkaian ac (alternating current) yang sinyalnya berupa sinusoidal, untuk menyelesaikan permasalahan pada sinusoidal digunakanlah fasor, hal ini pertama kali diusulkan oleh Charles Steinmetz pada tahun 1893, seorang matematikawan dan insinyur teknik elektro. Sebelum mambahas fasor, kita mengingat kembali bilangan kompleks.
Bilangan kompleks
Suatu bilangan kompleks pada bentuk kartesian (rectangular form) memiliki persamaan sebagai berikut:
\( z=+jy \)……………………………………………………..(1)
Dimana \( j=\sqrt{-1} \),
\( x \) adalah bagian riil dari bilangan kompleks \( z \)
\( y \) adalah bagian imajiner dari bilangan kompleks \( z \)
Bilangan kompleks juga bisa ditulis dalam bentuk polar:
\( z=r\angle \phi \)………………………………………………………(2)
Dimana \( r \) adalah besarnya \( z \)
\( \phi \) adalah fasa dari \( z \)
Bilangan kompleks bisa juga ditulis dalam bentuk eksponensial:
\( z=r e^{j\phi} \)……………………………………………………..(3)
Hubungan antara bentuk kartesian dan bentuk polar
Relasi kedua bentuk (polar dan kartesian) dapat dilihat pada gambar di bawah ini:
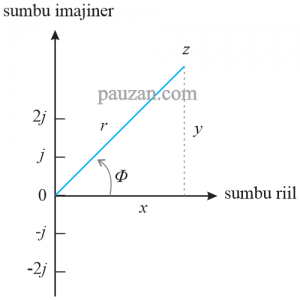
Gambar 1. Representasi dari bilangan kompleks \( z \) dalam bentuk kartesian dan polar
Baerdasarkan gambar 1, sumbu \( x \) merepresentasikan bagian riil dan sumbu \( y \) merepresentasikan bagian imajiner dari \( z \). Dengan menggunakan konsep sinus-cosinus maka;
\( \cos \phi=\frac{x}{r} \)\( x=r \cos \phi \)…………………………………………………(4)
Sedangkan;
\( \sin \phi=\frac{y}{r} \)\( y=r \sin \phi \)……………………………………………………(5)
Perhatikan bahwa berdasarkan rumus Pytagoras;
\( r=\sqrt{x^2+y^2} \)………………………………………….(6)
Sedangkan besarnya sudut \( \phi \) dapat diketahui melalui persamaan:
\( \phi=tan^{-1} \frac{y}{x}\)………………………………………………(7)
Berdasarkan persamaan (4) dan (5), bentuk kartesian dari \( z \) dapat ditulis sebagai berikut:
\( z=r(\cos \phi + j \sin \phi) \)………………………………….(8)
Operasi matematika pada bilangan kompleks
Jika kita ingin menjumlahkan atau mengurangi dua atau lebih bilangan kompleks, maka sebaiknya bilangan kompleks dalam bentuk kartesian. Tapi jika ingin mengalikan atau membagi antara dua atau lebih bilangan kompleks maka cara yang mudah adalah membuatnya dalam bentuk polar. Misalkan kita punya dua buah kompleks sebagai berikut:
\( z_1=x_1+jy_1 \)\( z_2=x_2+jy_2 \)
Bentuk polarnya:
\( z_1=r_1 \angle \phi_1 \) \( z_2=r_2 \angle \phi_2 \)
Bagaimana cara menjumlahkan, mengurangi, mengalikan dan membagi kedua bilangan kompleks tersebut?
Jawab
Penjumlahan:
\( z_1+z_2=x_1+jy_1+x_2+jy_2 \)\( z_1+z_2=(x_1+x_2 )+j(y_1+y_2 ) \)…………………………………………(9)
Pengurangan:
\( z_1-z_2=x_1+jy_1-(x_2+jy_2 ) \)\( z_1-z_2=(x_1-x_2 )+j(y_1-y_2 ) \)………………………………..(10)
Perkalian:
\( z_1z_2=r_1r_2 \angle (\phi_1+\phi_2) \)………………………………….(11)
Pembagian:
\( \frac{z_1}{z_2}=\frac{r_1}{r_2}\angle (\phi_1-\phi_2) \)……………………………….(12)
Persamaan-persamaan lain yang penting
Resiprokal:
\( \frac{1}{z}=\frac{1}{r} \angle -\phi \)……………………………………………………….(13)
Akar pangkat:
\( \sqrt{z}=\sqrt{r} \angle (\phi/2) \)………………………………………………………..(14)
Konjugat kompleks:
\( z*=x-jy \)……………………………………………………….(15)
Atau
\( z*=r \angle -\phi \)
Atau
\( z*=r e^{-j\phi} \)
Bentuk ;
\( \frac{1}{j}=-j \)…………………………………………………(16)
Fasor
Sebelum mengetahui bentuk fasor seperti apa, perhatikan identitas Euler berikut ini:
\( e^{\pm j\phi}=\cos \phi \pm j \sin \phi \)…………………………………………..(17)
Berdasarkan persamaan (17), bagian riil adalah cosinus dan bagian imajinernya adalah sinus, maka dapat ditulis:
\( \cos \phi=Ri(e^{j\phi} ) \)………………………………………………….(18)
\( \sin \phi=Im(e^{j\phi} ) \)………………………………………………………(19)
\( Ri \) berarti bagian riil dan \( Im \) berarti bagian imajiner.
Misalkan sebuah sinusoidal berbentuk:
\( v(t)=V_m \cos (\omega t+\phi) \)
Bagaimana \( v(t) \) dalam bentuk fasornya?
Jawab
Karena berbentuk cosinus maka berdasarkan persamaan (18) sinusoidal ini adalah bagian riil dari bilangan kompleks, sehingga:
\( v(t)=V_m Ri(e^{j(\omega t+\phi)} ) \)\( v(t)=Ri(V_m e^{j(\omega t+\phi)} ) \)
Ingat:
\( e^{a+b}=e^{a}e^{b} \)
Maka;
\( v(t)=Ri(V_m e^{j\phi} e^{j\omega t}) \)
Misalkan:
\( \vec{V}=V_m e^{j\phi} \)……………………………………………………(20)
Maka;
\( v(t)=Ri(\vec{V} e^{j\omega t} ) \)…………………………………………………….(21)
Persamaan (20) adalah representasi fasor dari \( v(t) \), dalam bentuk polar fasor \( \vec{V} \) berbentuk;
\( \vec{V}=V_m \angle \phi \)……………………………………….(22)
Berdasarkan persamaan (20) dan (21), \( \vec{V} \) adalah fasor dari \( v(t) \), fasor merupakan bilangan kompleks yang besar amplitudonya \( V_m \) dan arahnya adalah \( \phi \).
Soal: Bagaimanakah cara merepresentasikan fasor berikut ini ke dalam diagram fasor?
\( \vec{V}=V_m \angle \phi \)\( \vec{I}=I_m \angle -\theta \)
Jawab
Untuk tegangan, bentuk kartesiannya adalah;
\( \vec{V}=V_m (\cos \phi +j \sin \phi) \)
Sumbu riilnya adalah \( \cos \phi \), diplot sebagai sumbu horizontal dan \( \sin \phi \) adalah bagian imajiner, pada sumbu vertikal.
Catatan:
- Jika fasanya positif maka perputaran berlawanan jarum jam
- Jika fasanya negatif maka perputarannya searah jarum jam.
Maka diagram fasor untuk \( \vec{V} \) dapat dilihat pada gambar di bawah ini. Dengan cara yang sama, fasor \( \vec{I} \) juga diperoleh:
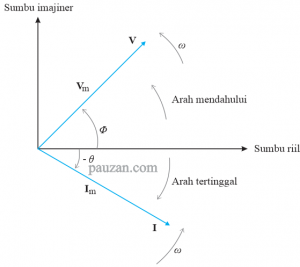
Gambar 2. Diagram fasor dari \( \vec{V}=V_m \angle \phi \) dan \( \vec{I}=I_m \angle -\theta \)
Perhatikan bahwa jika arah perputarannya searah jarum jam maka dikatakan sebagai arah yang tertinggal, tapi jika berlawanan arah jarum jam maka dikatakan sebagai arah mendahului. Hal yang perlu diperhatikan bahwa jika kita ingin merepresentasikan suatu sinusoidal ke dalam bentuk fasor maka yang pertama dilakukan adalah mengubah bentuknya ke bentuk cosinus.
Misalkan suatu sinusoidal;
\( v(t)=V_m \cos (\omega t+\phi) \)
Tentukan \( dv/dt \)
Jawab
\( \frac{dv}{dt}=\frac{d}{dt}(V_m \cos (\omega t+\phi)) \)
Ingat;
\( \frac{d}{dt}(\cos At)=-A \sin At \)
Maka;
\( \frac{dv}{dt}=-\omega V_m \sin (\omega t+\phi) \)
Karena kita ingin representasikan ke fasor, maka kita rubah bentuknya ke cosinus. Ingat:
\( +\cos (\omega t+90^{o})=-\sin \omega t \)
Maka;
\( \frac{dv}{dt}=\omega V_m \cos (\omega t+\phi+90^{o}) \)
Ingat;
\( Ri(e^{j(\omega t+\phi+90^{o})} )=\cos (\omega t+\phi+90^{o}) \)
Maka;
\( \frac{dv}{dt}=Ri(\omega V_m e^{j(\omega t+\phi+90^{o})}) \) \( \frac{dv}{dt}=Ri(\omega V_m e^{j\omega t}e^{j\phi}e^{j90^{o}} ) \)Ingat:
\( e^{j90^{o}}=\cos 90^{o}+j \sin 90^{o}=j \)
Maka;
\( \frac{dv}{dt}=Ri(j\omega \vec{V}e^{j\omega t} ) \)…………………………………..(23)
Berdasarkan persamaan (23), dengan menggunakan fasor kita berhasil merubah yang sebelumnya sinusoidal tergantung waktu menjadi sinusoidal tergantung fasor. Perhatikan transformasinya;
\( \frac{dv}{dt} \Leftrightarrow j\omega \vec{V} \)………………………………(24)
Dengan cara yang sama, jika kita integralkan \( v(t) \) diperoleh transformasi;
\( \int vdt \Leftrightarrow \frac{\vec{V} }{j\omega} \)……………………………..(25)
Persamaan (24) dan (25) sangat berguna pada saat kita ingin mengetahui solusi dari keadaan steady-state. Berdasarkan pembahasan yang telah kita lakukan, maka dapat dismpulkan perbedaan antara \( v(t) \) dengan \( \vec{V} \);
- \( v(t) \) adalah fungsi waktu, sedangkan \( \vec{V} \) adalah fungsi frekuensi atau fasor
- \( v(t) \) tergantung pada waktu, sedangkan \( \vec{V} \) tidak.
- \( v(t) \) selalu dalam bentuk riil sedangkan \( \vec{V} \) pada umumnya berbentuk bilangan kompleks.
Contoh soal 1 (Bilangan Kompleks)
Hitunglah bilangan kompleks berikut ini:
1.\( 40\angle 50^{o}+20\angle -30^{o} \)
2.\( \frac{10\angle -30^{o}}{2+j4} \)
Jawab
1.Karena penjumlahan maka dirubah ke bentuk kartesian
\( 40 \angle 50^{o} \)Bentuk kartesiannya adalah;
\( 40 \angle 50^{o}=40(\cos 50^{o}+j \sin 50^{o}) \)\( \cos 50^{o}=0,64 \)
\( \sin 50^{o}=0,77 \)
Maka;
\( 40(\cos 50^{o}+j \sin 50^{o})=40(0,64+j0,77) \)\( 40 \angle 50^{o}=25,6+j30,8 \)
\( 20 \angle -30^{o} \);
Bentuk kartesiannya adalah;
\( 20 \angle -30^{o}=20(\cos -30^{o}+j \sin -30^{o}) \)\( 20 \angle -30^{o}=20(0,867+j(-0,5)) \)
\( 20 \angle -30^{o}=17,34-j10 \)
Maka penjumlahannya adalah;
\( 40 \angle 50^{o}+20 \angle -30^{o}=25,6 +j17,34-j10 \)\( 40 \angle 50^{o}+20 \angle -30^{o}=(25,6+17,34)+j(30,8-10) \)
\( 40 \angle 50^{o}+20 \angle -30^{o}=42,94+j20,8 \)
2. Karena pembagian maka dirubah ke bentuk polar
Karena hanya penyebut yang berbentuk sinusoidal, maka kita rubah bentuknya ke polar;
\( 2+j4 \)Dari persamaan di atas, \( x=2, y=4 \)
Mencari \( r \)
\( r=\sqrt{x^2+y^2}=\sqrt{4+16} \)\( r=\sqrt{20}=4,47 \)
Mencari fasa \( \phi \)
\( \phi=tan^{-1} \frac{y}{x}=tan^{-1}\frac{4}{2} \)\( \phi=tan^{-1} 2=63,43^{o} \)
Jadi;
\( 2+j4=4,47 \angle 63,43^{o} \)
Pembagiannya menjadi;
\( =\frac{10\angle -30^{o}}{4,47 \angle 6,43^{o}} \)
Berdasarkan persamaan (9), maka;
\( =\frac{10}{4,47}\angle (-330^{o}-63,43^{o}) \)\( =2,37 \angle -93,43^{o} \)
Dirubah bentuk ke sinusoidal;
\( \frac{10\angle -30^{o}}{2+j4}=2,37 (\cos -93,43^{o}+j \sin -93,43^{o}) \)
Contoh soal 2 (sinusoidal ke fasor)
Transformasikan sinusoidal berikut ini ke dalam bentuk fasor
1. \( i=6 \cos (50t-40^{o}) \) A
2.\( v=-4 \sin (30t+50^{o}) \) V
Jawab
1.Bentuk umum dari persamaan arus \( i \) adalah;
\( i=I_m \cos (\omega t+\phi) \)Maka berdasarkan soal, amplitdonya sebesar:
\( I_m=6 \)
Fasanya sebesar;
\( \phi=-40^{o} \)
Jadi bentuk fasornya adalah:
\( \vec{I}=I_m \angle \phi \)
\( \vec{I}=6 \angle -40^{o} \) A
2. Bentuk gelombangnya adalah sinus, maka pertama kita harus transformasikannnya ke cosinus.
Pada pembahasan tentang sinusoidal, didapatkan persamaan:
\( +\cos (\omega t+90^{o})=-\sin \omega t \)
Misal: \( \beta=30t+50^{o} \), maka:
\( +\cos (\beta+90^{o})=-\sin \beta \)
Persamaan tegangan menjadi;
\( v=-4 \sin (30t+50^{o})=4 \cos (30t+50^{o}+90^{o}) \)\( v=4 \cos (30t+140^{o}) \)
Diperoleh amplitudo;
\( V_m=4 \)
Fasanya;
\( \phi=140^{o} \)
Sehingga bentuk fasornya adalah:
\( \vec{V}=V_m \angle \phi \)\( \vec{V}=V_m \angle \phi \)
\( \vec{V}=4 \angle 140^{o} \)
Contoh Soal 3 (fasor ke sinusoidal)
Carilah bentuk sinusoidal pada fasor berikut ini:
1.\( \vec{I}=-3+j4 \) A
2.\( \vec{V}=j8 e^{-j20^{o}}\) V
Jawab
1.Bentuknya adalah kartesian, maka dirubah ke polar
Berdasarkan soal, diperoleh;
\( x=-3 \)\( y=4 \)
Maka besarnya \( r \) adalah;
\( r=\sqrt{x^2+y^2}=\sqrt{(-3)^2+(4)^2} \)\( r=\sqrt{25}=5 \)
Menentukan fasa;
\( \phi=\tan^{-1} \frac{y}{x} \)\( \phi=\tan^{-1} -\frac{4}{3} \)
\( \phi=-53,13^{o} \)
Maka bentuk polarnya adalah:
\( \vec{I}=5\angle -53,13^{o} \)
bentuk sinusoidalnya adalah:
\( i(t)=I_m \cos (\omega t+\phi) \)
Maka;
\( i(t)=5 \cos (\omega t-53,13^{o}) \) A
2.Bentuknya adalah eksponensial maka dirubah ke polar
Untuk \( 8e^{-j20^{o}} \)
\( 8e^{-j20^{o}}=re^{j\phi} \)
Jadi
\( r=8 \)\( \phi=-20^{o} \)
Jadi bentuk polarnya adalah;
\( 8e^{-j20^{o}}=r\angle \phi \)\( 8e^{-j20^{o}}=8\angle -20^{o} \)
Untuk \( j \)
Misalkan suatu sinusoidal;
\( 1(\cos 90^{o}+j \sin 90^{o})=1(0+j) \)\( 1(\cos 90^{o}+j \sin 90^{o})=j \)
Jadi kita bisa merubah bentuk \( j \) menjadi fungsi sinusoidal, maka bentuk polarnya adalah:
\( 8e^{-j20^{o}} =r\angle \phi \)\( 8e^{-j20^{o}} =1\angle 90^{o} \)
Maka \( j8e^{-j20^{o}} \) adalah;
\( 8e^{-j20^{o}}=1\angle 90^{o} (8\angle -20^{o}) \)
Dengan menggunakan rumus perkalian bilangan kompleks, maka;
\( r_1\angle \phi_1 (r_2\angle \phi_2 )=r_1 r_2∠(\phi_1+\phi_2) \)\( =8\angle (90^{o}-20^{o}) \)
\( =8\angle 70^{o} \)
Kita konversi ke bentuk sinusoidal;
\( v(t)=8 \cos (\omega t+70^{o}) \) V
Contoh Soal 4 (penjumlahan sinusoidal)
Diberikan dua buah arus dengan persamaan:
\( i_1 (t)=4 \cos (\omega t+30^{o}) \) A
\( i_2 (t)=5 \sin (\omega t-20^{o}) \) A
Berapakah hasil dari penjumlahannya?
Jawab
Ingat: operasi apapun pada sinusoidal (penjumlahan, pengurangan, perkalian dan pembagian) akan lebih mudah dilakukan jika dirubah bentuk ke fasor.
Samakan bentuk sinusoidal ke cosinus
Arus \( i_1 \) berbentuk cosinus, sedangkan arus \( i_2 \) berbentuk sinus. Kita transformasi \( i_2 \) ke bentuk cosinus;
Ingat persamaan yang kita dapatkan pada pembahasan tentang sinusoidal:
\( +\cos (\omega t-90^{o})=+\sin (\omega t) \)
Oleh karena itu, supaya menjadi cosinus, dikurangi sudut \( 90^{o} \);
\( 5 \sin (\omega t-20^{o})=5 \cos (\omega t-20^{o}-90^{o}) \)\( =5 \cos (\omega t-110^{o}) \)
Ubah ke fasor
Untuk \( i_1 \)
Diketahui;
\( I_m=4 \)\( \phi=30^{o} \)
Maka;
\( \vec{I_1}=4\angle 30^{o} \)
Untuk \( i_2 \)
Diketahui;
\( I_m=5 \)\( \phi=-110^{o} \)
Maka;
\( \vec{I_2}=5\angle (-110^{o}) \)
Penjumlahan keduanya adalah;
\( \vec{I}=\vec{I_1}+\vec{I_2} \)\(\vec{I}=4 \angle 30^{o} +5 \angle (-110^{o}) \)
Karena panjumlahan maka kita rubah ke bentuk kartesian;
\( 4\angle 30^{o} \);
\( r=4 \)
Mencari \( x \);
\( x=r \cos \phi=4 \cos 30^{o} \)\( x=4(\frac{1}{2}\sqrt{3} )=3,46 \)
Mencari \( y \);
\( y=r \sin \phi \)\( y=4 \sin 30^{o}=4 (0,5) \)
\( y=2 \)
Bentuk kartesian adalah;
\( z=x+jy \)
Jadi
\( \vec{I_1}=3,46+j2 \)
\( 5\angle (-110^{o}) \);
\( r=5 \)
Mencari \( x \);
\( x=5 \cos (-110^{o})=-1,71 \)
Mencari \( y \);
\( y=5 \sin (-110^{o})=-4,70 \)
Jadi;
\( \vec{I_2}=-1,71-j4,70 \)
Maka penjumlahannya menjadi;
\(\vec{I}=3,46+j2-1,71-j4,70 \)
\( \vec{I}=(3,46-1,71)+j(2-4,70) \)
\( \vec{I}=1,75-j2,70 \)
kita rubah ke bentuk polar;
\( I_m=\sqrt{(1,75)^2+(-2,70)^2}=\sqrt{3,0625+7,29} \)\( I_m=3,28 \)
Fasanya;
\( \phi=tan^{-1}\frac{y}{x}=tan^{-1}\frac{-2,70}{1,75} \)\( \phi=tan^{-1} (-1,543)=-57,05^{o} \)
Kita rubah bentuknya ke sinusoidal:
\( i(t)=I_m \cos (\omega t+\phi) \)
\( i(t)=3,28 \cos (\omega t-57,05^{o}) \) A
Contoh Soal 5 (sinusoidal yang memiliki turunan atau integral)
Gunakanlah pendekatan fasor untuk menghitung persamaan arus \( i(t) \) pada persamaan di bawah ini:
\( 4i+8\int idt-3 \frac{di}{dt}=50 \cos (2t+75^{o}) \)
Jawab
Suku kiri maupun kanan merupakan persamaan sebagai fungsi waktu, maka langkah pertama yang dilakukan adalah emrubahnya menjadi fungsi fasor
Merubah ke bentuk fasor
Untuk ruas kiri:
\( 4i=4 \vec{I} \)
Kenapa bisa langsung diubah ke \( \vec{I} \)?
Berdasarkan soal, sudah pasti arus \( i \) berbentuk sinusoidal (perhatikan hasilnya, berada di suku kanan berupa suatu sinusoidal). Jadi bentuknya secara umum:
\( i(t)=I_m \cos (\omega t+\phi) \)
Representasinya dalam bentuk fasor adalah;
\( \vec{I}=I_m\angle \phi \)
Kemudian \( 8\int idt \);
Berdasarkan persamaan (24), suatu sinusoidal ( bisa diganti dengan apapun selama sama-sam berbentuk sinusoidal) jika diintegralkan menghasilkan;
\( \int idt=\frac{\vec{I} }{j \omega} \)
Maka;
\( 8\int idt=\frac{8\vec{I} }{j \omega} \)
Kemudian \( 3 di/dt \);
Berdasarkan persamaan (23);
\( 3 \frac{di}{dt}=3j\omega \vec{I} \)
Untuk ruas kanan:
\( 50 \cos (2t+75^{o})=50\angle 75^{o} \)
Jadi bentuk fasor dari soal di atas adalah;
\( 4 \vec{I}+\frac{8 \vec{I} }{j \omega}-3j\omega \vec{I}=50 \angle 75^{o} \)
Nilai \( \omega=2 \), maka;
\( 4 \vec{I}+\frac{8 \vec{I} }{j2}-j6 \vec{I}=50 \angle 75^{o} \)\( \vec{I}(4+\frac{8}{j2}-j6)=50 \angle 75^{o} \)
Ingat:
\( \frac{1}{j}=-j \)Maka;
\( \vec{I}(4-j4-j6)=50\angle 75^{o} \)\( \vec{I}=\frac{50∠75^{o}}{4-j10} \)
Karena bentuknya pembagian, maka dirubah bentuk ke polar. Jadi yang dirubah hanya penyebutnya:
\( 4-j10=r\angle \phi \)
Mencari \( r \)
\( r=\sqrt{s^2+y^2}=\sqrt{16+100} \)\( r=\sqrt{116}=10,77 \)
Mencari fasa;
\( \phi=tan^{-1}\frac{y}{x}=tan^{-1}\frac{-10}{4} \)\( \phi=tan^{-1} (-2,5)=-68,2^{o} \)
Jadi;
\( 4-j10=10,77\angle (-68,2^{o}) \)
Maka;
\(\vec{I} =\frac{50 \angle 75^{o}}{(10,77 \angle (-68,2^{o}) }=\frac{50}{10,77} \angle (75^{o}-(-68,2^{o})) \)
\(\vec{I}=4,64 \angle 143,2^{o} \) A
Kita rubah ke bentuk sinusoidal:
\( i(t)=4,64 \cos (2t+143,2^{o}) \) A
PREVIOUS: Sinusoidal
NEXT: Persamaan fasor pada R, L dan C