Mahasiswa sering kesusahan dalam menentukan nilai awal dan akhir pada kasus rangkaian orde dua, misal menetukan \( dv/dt, di/dt \) atau menentukan arus steady state \( i(\infty) \) dan tegangan pada saat steady state \( v(\infty) \). Jadi sebelum kita masuk ke pembahasan rangkaian orde dua, terlebih dahulu kita mencoba menenetukan nilai awal dan akhir dari rangkaian tersebut.
Tips untuk menentukan kondisi awal dan akhir adalah:
- Saat dalam kondisi steady-state, kemudian sakelar ditutup atau dibuka maka tegangan pada kapasitor bersifat kontinyu, artinya sesaat sebelum dan sesaat setelah sakelar ditutup atau dibuka tegangannya dianggap sama:
- Berbeda dengan kapasitor, induktor memiliki arus yang kontinyu sesaat sebelum dan sesaat setelah sakelar ditutup atau dibuka:
Jadi dalam menentukan nilai awal, kita hanya fokus pada tegangan pada kapasitor dan arus pada induktor.
Selain itu, harus diingat bahwa:
- Saat kondisi steady-state kapasitor bersifat sebagai rangkaian terbuka (untuk sumber DC), dan induktor bersifat sebagai rangkaian pendek (short circuit).
Contoh Soal
Perhatikan rangkaian di bawah ini:
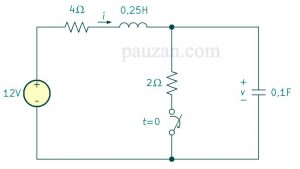
Gambar 1. Contoh soal cara mencari nilai awal dan akhir pada rangkaian orde dua
Sakelar pada gambar 1 sudah tertutup dalam jangka waktu yang lama, kemudian dibuka pada saat \( t=0 \), tentukanlah:
- \( i(0^+ ), v(0^+) \)
- \( \frac{di(0^+ )}{dt}, \frac{dv(0^+ )}{dt} \)
- \( i(\infty), v(\infty) \)
Jawab
-
Menentukan \( i(0^+) \) dan \( v(0^+) \)
Sakelar tertutup dalam waktu yang lama saat \( t<0 \), artinya rangkaian dalam kondisi steady-state, ingat pada kondisi ini induktor bersifat rangkaian pendek (short) dan kapasitor bersifat rangkaian terbuka. Maka rangkaian pada gambar 1 menjadi:
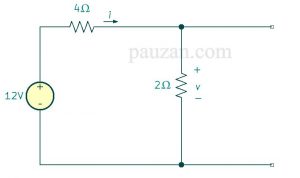
Gambar 2. Kondisi steady state saat \( t<0 \)
Berdasarkan gambar 2 kita bisa menentukan arus saat \( t<0 \) pada induktor dan tegangan saat \( t<0 \) pada kapasitor.
Arus yang melalui induktor sama saja besarnya dengan arus yang melewati resistor 4Ω, maka arus pada resistor tersebut adalah:
\( i=\frac{V}{R_{eq}} \)
\( R_{eq} \) adalah resistor seri antara 4Ω dengan 2Ω, maka \( R_{eq}=4+2=6\Omega \):
\( i=\frac{12}{6}=2 A \)Jadi arus pada induktor saat \( t<0 \) adalah:
\( i(0^- )=2 A \)
Tegangan pada kapasitor saat \( t<0 \):
Berdasarakan gambar 2, tegangan pada kapasitor paralel dengan resistor 2Ω, artinya besar tegangannya sama maka:
\( v_{2Ω}=iR=2 . 2=4 V \)Jadi tegangan pada kapasitor adalah:
\( v(0^- )=4 V \)
Saat sakelar dibuka:
Sesaat setelah sakelar dibuka, arus pada induktor dan tegangan pada kapasitor bersifat kontinyu, maka:
\( i(0^+ )=i(0^- )=2 A \) \( v(0^+ )=v(0^- )=4 V \)
-
Menentukan \( \frac{di(0^+ )}{dt}, \frac{dv(0^+ )}{dt} \)
Sesaat setelah sakelar dibuka, rangkaian pada gambar 1 menjadi:
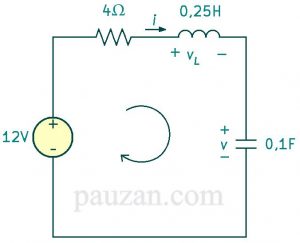
Gambar 3. Sesaat setelah sakelar dibuka (ditambahkan loop)
\( di(0^+)/dt \) mengacu pada arus induktor sesaat setelah sakelar dibuka. Persamaan tegangan pada induktor adalah:
\( v_L (0^+)=L \frac{di(0^+)}{dt} \)
\( L \) dipindah ruas maka:
\( \frac{di(0^+)}{dt}=\frac{v_L (0^+)}{L} \)
Mencari \( v_L (0^+) \) :
Berdasarkan gambar 3, \( v_L (0^+) \) dapat dicari menggunakan hukum tegangan Kirchhoff (KVL):
\( \Sigma V=0 \)
Dengan menggunakan loop searah jarum jam:
\( -12+v_{4Ω}+v_L+v=0 \)
\( -12+R i(0^+ )+v_L (0^+ )+v(0^+ )=0 \)
\( -12+4(2)+v_L (0^+ )+4=0 \)
\( -12+12+v_L (0^+ )=0 \)
\( v_L (0^+ )=0 \)
Jadi:
\( \frac{di(0^+)}{dt}=\frac{0}{L}=0 \)
\( dv(0^+)/dt \) mengacu pada tegangan pada kapasitor sesaat setelah sakelar dibuka. Rumus arus pada kapasitor adalah:
\( i_C (0^+)=C \frac{dv(0^+)}{dt} \)
\( C \) pindah ruas:
\( \frac{dv(0^+)}{dt}=\frac{i_C (0^+)}{C} \)
Mencari \( i_C (0^+) \):
Berdasarkan gambar 3, arus yang melalui induktor sama besarnya dengan arus yang menuju kapasitor, artinya:
\( i_C (0^+ )=i(0^+ )=2 A \)
Jadi:
\( \frac{dv(0^+)}{dt}=\frac{2}{0,1}=20 V/s \)
-
Menentukan \( i(\infty) \) dan \( v(\infty) \)
\( i(\infty) \) dan \( v(\infty) \) adalah kondisi rangkaian mencapai steady-state, ingat pada keadaan ini induktor bersifat rangkaian short sedangkan kapasitor bersifat rangkaian terbuka. Rangkaian pada gambar 1 menjadi:
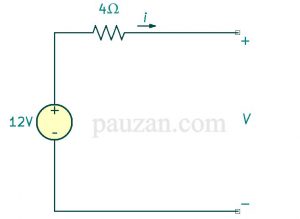
Gambar 4. Rangkaian saat mencapai kondisi steady-state
Berdasarkan gambar 4, arus yang melalui induktor sama dengan arus yang melalui resistor 4Ω, karena rangkaian bersifat terbuka maka tidak ada arus yang melalui resistor, jadi arus yang melalui induktor adalah:
\( i(\infty)=0 \)Berdasarkan gambar 4, tegangan pada kapasitor paralel dengan sumber 12V, kenapa resistor 4Ω tidak dianggap? Karena rangkaian bersifat terbuka, artinya resistor tersebut dapat digantikan dengan kabel biasa. Jadi tegangan pada kapasitor saat mencapai steady-state adalah:
\( v(\infty)=12 V \)
NEXT: Rangkaian Seri RLC