Multiplexing adalah mengirimkan informasi yang besar menjadi jumlah yang lebih kecil. Berdasarkan hal tersebut digital multiplexer berarti rangkaian kombinasi yang menyeleksi satu dari sekian banyak informasi biner dan hanya menghasilkan satu garis output. Oleh karena itu multiplexer disebut juga sebagai data selector. Pemilihan satu input ini menggunakan garis seleksi yang berlambang S. Jika terdapat \(2^n\) input maka terdapat n garis seleksi.
Mari kita coba membuat 4×1 multiplexer, terdapat 4 input maka ada berapa n? \(2^n=4\), maka nilai n yang sesuai adalah 2, jadi terdapat 2 seleksi. Multiplexer biasanya disebut MUX, perhatikan diagram blok multiplexer di bawah ini:
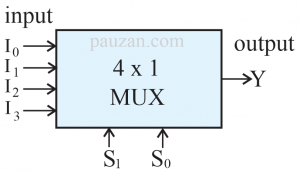
Gambar 1. Diagram blok 4×1 multiplexer
Misalkan inputnya berupa \(I_0,I_1,I_2,I_3\) dengan garis seleksi \(S_0\) dan \(S_1\) dan outputnya Y. Selanjutnya kita membuat tabel kebenaran, tapi khusus untuk multiplexer variabel inputnya tidak ditulis melainkan hanya garis seleksinya saja yaitu \(S_0\) dan \(S_1\). Dengan dua garis seleksi maka ada berapa kombinasi yang diperoleh? Karena biner maka 2 dipangkat dengan banyaknya garis seleksi, yaitu \(2^2=4\) kombinasi. Tabel kebenarannya menjadi:
Tabel 1. Tabel kebenaran 4 input multiplexer
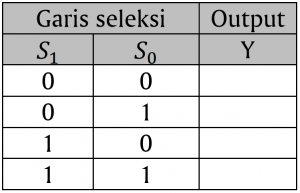
Ingat \(I_0\) bernilai desimal 0, begitu seterusnya sampai \(I_3\) bernilai 3. Jadi pada garis seleksi \(S_0=0, S_1=0\) maka desimal dari garis seleksi ini adalah \(S_0:2^0×0=0, S_1=2^1×0=0\) maka \(S_0+S_1=0+0=0\). Jadi input yang bernilai 0 adalah \(I_0\), oleh karena itu outputnya adalah \(I_0\). Kita coba \(S_0=1,S_1=0\) maka \(S_0:2^0×1=1,S_2:2^1×0=0\) maka \(S_0+S_1=1+0=1\). Input yang bernilai decimal 1 adalah \(I_1\) maka nilai di output Y adalah \(I_1\). Langkah ini terus dilakukan sampai ke kombinasi terakhir, akhirnya tabel kebenaran dari 4×1 MUX adalah:
Tabel 2. Tabel kebenaran 4×1 MUX
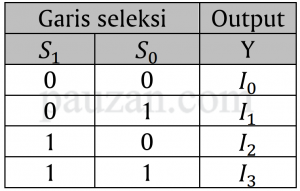
Dari tabel kebenaran di atas, kita dapat menuliskan fungsi Booleannya untuk output Y. Dipilih bentuk perkalian jumlah (ekspansi sukumin), maka yang bernilai 0 akan dikomplemenkan. Untuk kombinasi pertama, \(S_0\) dan \(S_1\) bernilai 0 maka bagian pertama outputnya adalah \(I_0 S’_0 S’_1\), begitu seterusnya sehingga persamaan Booleannya menjadi:
\(Y=I_0 S’_0 S’_1+I_1 S_0 S’_1+I_2 S’_0 S_1+I_3 S_0 S_1\)
Dari persamaan di atas, selanjutnya kita gambar rangkaian gerbang logikanya. Perhatikan rangkaian berikut ini:
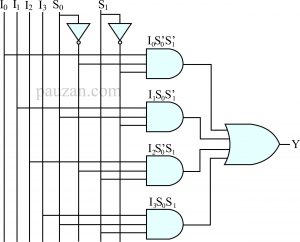
Gambar 2. Rangkaian gerbang logika untuk 4×1 MUX