Perhatikan gambar di bawah ini:
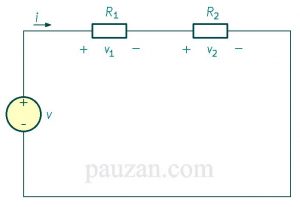
Gambar 1. Rangkaian pembagi tegangan
Berdasarkan gambar 1, arus yang melalui \( R_1 \) maupun \( R_2 \) adalah sama karena tidak ada percabangan arus. Kita terapkan hukum Ohm maka tegangan untuk tiap resistor adalah:
\( v_1=iR_1, v_2=iR_2 \)………………………………..(1)
Sekarang kita terapkan hukum tegangan Kirchhoff (KVL), perhatikan gambar loop pada rangkaian di bawah ini:
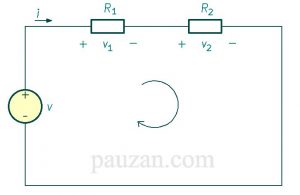
Gambar 2. Loop pada rangkaian
Berdasarkan gambar 2, maka KVL:
\( \Sigma v=0 \)\( -v+v_1+v_2=0 \)
\( v=v_1+v_2 \)……………………………………………………….(2)
Sekarang kita subtitusikan persamaan (1) maka:
\( v=iR_1+iR_2=i(R_1+R_2) \)
\( i=\frac{v}{R_1+R_2}\)……………………………………………..(3)
Dengan mensubtitusikan persamaan , tegangan pada resistor pertama adalah:
\( v_1=\frac{v}{R_1+R_2}R_1 \)
\( v_1=\frac{R_1}{R_1+R_2}v \)…………………………………(4)
Dengan cara yang sama, teganga pada resistor kedua adalah:
\( v_2=\frac{v}{R_1+R_2}R_2\)
\( v_2=\frac{R_2}{R_1+R_2}v \)……………………………..(5)
Contoh soal
Perhatikan rangkaian di bawah ini:
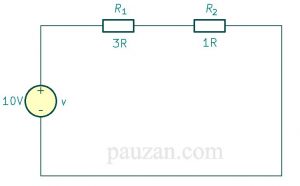
Gambar 3. Soal rangkaian pembagi tegangan
Tentukanlah tegangan pada resistor \( R_1 \) dan \( R_2 \)
Jawab
Tegangan pada \( R_1 \)diperoleh dengan menerapkan persamaan (4):
\( v_1=\frac{3}{3+1}10=\frac{30}{4}=7,5 A \)
Tegangan pada \( R_2 \) dapat diperoleh dengan menggunakan persamaan (5), maka:
\( v_2=\frac{1}{3+1}10=2,5 V \)