Hukum Kirchhoff jika diterapkan pada rangkaian resistif (hanya terdiri dari resistor) maka akan menghasilkan persamaan-persamaan aljabar, pemecahannya menggunakan aturan subtitusi atau dengan determinan matriks. Tapi jika Hukum Kirchhoff diterapkan pada rangkaian RC (resistor-kapasitor) atau RL (resistor-induktor) maka akan menghasilkan persamaan diferensial orde satu. Oleh karena itu rangkaian RC maupun RL disebut juga sebagai rangkaian orde satu. Kita mulai membahas dari rangkaian RC terlebih dahulu.
- Rangkaian RC sumber-bebas
Pada awalnya rangkaian ini terhubung oleh sumber tegangan DC, tapi kemudian sumber DCnya dilepaskan, pada saat itulah terjadinya rangkaian RC sumber-bebas. Setelah sumber dilepaskan maka energi yang tersimpan pada kapasitor akan dilepaskan ke resistor. Dengan mengasumsikan bahwa kapasitor pada rangkaian RC pada mulanya menyimpan muatan seperti pada gambar di bawah ini:
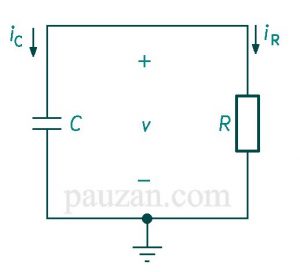
Gambar 1. Rangkaian RC sumber-bebas
Karena pada awalnya kapasitor terisi muatan, maka dapat diasumsikan bahwa saat tegangannya sebesar;
\( v(0)=V_0 \)………………………………………..(1)
Pada kondisi awal tersebut, energi yang tersimpan sebesar:
\( w(0)=\frac{1}{2}CV_0^2 \)…………………………………..(2)
Dengan menerapkan Hukum Arus Kirchhoff pada simpul atas pada gambar 1 di atas menghasilkan:
\( i_{masuk}=i_{keluar} \)Tidak ada arus masuk pada simpul, maka \( i_{masuk}=0 \);
\( 0=i_c+i_R \)…………………………………………………………………(3)
Mengingat bahwa;
\( i_C=C\frac{dv}{dt} \)dan
\( i_R=\frac{v}{R}\)Maka persamaan (3) dapat juga ditulis;
\( C \frac{dv}{dt}+\frac{v}{R}=0 \)…………………………………..(4.1)
Kedua ruas dikali \( 1/C \)maka;
\( \frac{dv}{dt}+\frac{v}{RC}=0 \)……………………………………(4.2)
Persamaan (4.2) adalah persamaan diferensial orde pertama.
Supaya dapat diselesaikan, v/RC dipindah ke ruas kanan;
\( \frac{dv}{dt}=\frac{-v}{RC}\)dt dipindah ke ruas kanan, v ke ruas kiri, hasilnya:
\( \frac{dv}{v}=\frac{-1}{RC}dt \)…………………………………(5)
Kita integralkan kedua ruas, hasilnya;
\( \ln v=\frac{-t}{RC}+\ln A \)……………………………………….(6)
\(ln A \)adalah konstanta integrasi, kita pindah ke ruas kiri maka;
\( \ln v-\ln A=\frac{-t}{RC} \)
Ingat: \( \ln X-\ln Y=\ln \frac{X}{Y} \) maka;
\( \ln \frac{v}{A}=\frac{-t}{RC} \)…………………………….(7)
Kita rubah bentuk ke e maka;
\( v(t)=Ae^{\frac{-t}{RC}} \)………………………………………………….(8)
Ingat kondisi awalnya adalah \( v(0)=A=V_0 \), maka;
\( v(t)=V_0 e^{\frac{-t}{RC}} \)……………………………………..(9)
Berdasarkan persamaan (9), respon tegangan pada rangakaian RC merupakan penurunan eksponensial dari tegangan awal \( V_0 \). Respon tegangan ini disebabkan oleh energi tersimpan pada kapasitor tanpa adanya pengaruh dari sumber eksternal baik sumber tegangan atau sumber arus. Kondisi ini disebut sebagai respon alami (natural response) dari rangkaian.
Respon alami dari rangkaian RC dapat dilihat pada gambar berikut ini:
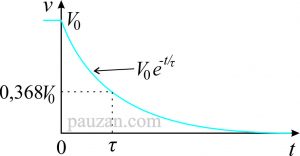
Gambar 2. Respon alami dari rangkaian RC
Pada saat \( t=0 \), tegangannya sama besarnya dengan tegangan pada persamaan (9). Seiring pertambahan waktu t tegangannya menurun drastis secara eksponensial. Penurunan tegangan ini diekspresikan dalam bentuk konstanta waktu (time constant), lambangnya τ. Besarnya τ adalah:
\( \tau=RC \)………………………………………(10)
RC diganti τ pada persamaan (9), maka hasilnya:
\( v(t)=V_0 e^{\frac{-t}{\tau}} \)……………………………………..(11)
Jika τ dimasukkan ke persamaan (9) untuk menggantikan t maka;
\( v(τ)=V_0 e^{\frac{-τ}{RC}}=V_0 e^{-1}=0,368V_0 \)
Tegangan pada saat waktu t=τ tersebut dapat dilihat pada gambar 2 di atas.
Dengan perhitungan yang sama, nilai konstanta waktu 2τ, 3τ sampai 5τ dapat dilihat pada tabel di bawah ini:
Tabel 1. Nilai tegangan yang berkaitan dengan konstanta waktu
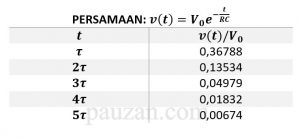
Berdasarkan persamaan (9) dan (10) di atas, kita dapat mencari arus yang melalui resistor:
\( i_R=\frac{v(t)}{R}=\frac{V_0 e^{\frac{-t}{ τ}}}{R} \)…………………(12)
Daya yang terdisipasi pada resistor sebesar:
\( p(t)=vi_R=(V_0 e^{{-t}{τ}} )(\frac{V_0e^{\frac{-t}{ τ}}}{R} ) \)\( p(t)=\frac{V_0^2e^\frac{-2t}{τ}}{R} \)………………………………………….(13)
Sedangkan energi yang didapatkan oleh resistor sebagai fungsi waktu adalah:
\( w_R (t)=\int_{0}^{t}p dt=\int_{0}^{t}\frac{V_0^2e^\frac{-2t}{τ}}{R} dt \)\( w_R (t)=-\frac{τV_0^2}{2R} e^\frac{-2t}{τ}]_0^t \)
memasukkan τ=RC, maka:
\( w_R (t)=\frac{1}{2}CV_0^2 (1-e^\frac{-2t}{τ} ) \)…………………………………(14)
Contoh Soal 1
Perhatikan rangkaian di bawah ini:
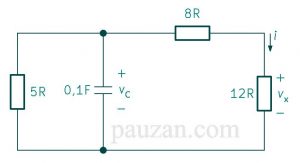
Gambar 3. Soal RC sumber-bebas
Jika \( v_C (0)=15 \)V, tentukan \( v_C, v_x, i_x\) pada t=1.
Jawab
Supaya bisa menjawab, terlebih dahulu kita rubah bentuknya menjadi seperti pada gambar 1 yaitu hanya ada satu R dan kapasitor. Berdasarkan gambar 3, resistor 8 Ω dengan 12 Ω tersusun seri, resistansi ekivalennya adalah:
\( R_s=8+12=20 Ω \)Rangkaiannya menjadi:
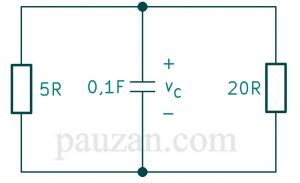
Gambar 4. Rangkaian setelah 8 dan 12 Ω diseri
Gambar 4 juga bisa digambar menjadi bentuk seperti di bawah ini:
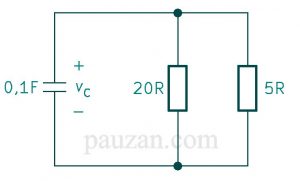
Gambar 5. Bentuk lain rangkaian pada gambar 4
Berdasarkan gambar 5, \( R_s \) dan 5 Ω tersusun paralel maka:
\( \frac{1}{R_p}=\frac{1}{5}+\frac{1}{R_s} =\frac{1}{5}+\frac{1}{20} \)\( \frac{1}{R_p} =\frac{5}{20} \)
\( R_p=4 Ω \)
Sekarang rangkaiannya menjadi:
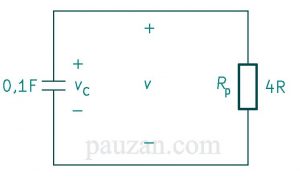
Gambar 6. Rangkaian dengan R tunggal
Gambar 6 sama bentuknya dengan gambar 1, sekarang kita bisa melakukan perhitungan.
Mengacu pada persamaan (10), maka konstanta waktunya adalah:
\( τ=RC \)\( τ=R_p C=4 . 0,1=0,4 \)detik
Selanjutnya mencari tegangan pada gambar 6 dengan menggunakan persamaan (11):
\( v(1)=V_0 e^{\frac{-1}{τ}} \)\( v(1)=15e^{\frac{-t}{0,4}}=15e^{-2,5} \) volt
Mencari \( v_C \)
Mengacu pada gambar 6, tegangan v sama besarnya dengan tegangan pada kapasitor (\(v_C \)) maupun tegangan pada \( R_p \), maka;
\( v=v_C=15e^{-2,5} \) volt
Mencari \( v_x \)
Rangkaian pada gambar 3 dapat juga dibuat seperti berikut ini:
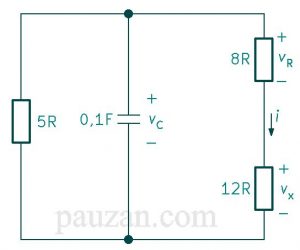
Gambar 7. Rangkain pada gambar 6 dibuat dalam bentuk berbeda
Parhatikan gambar 7, tegangan pada resistor 12 Ω dapat dicari dengan menggunakan konsep rangkaian pembagi tegangan. Sehingga tegangan pada 12 Ω adalah:
\( v_x=\frac{12}{8+12} v=0,6(15e^{-2,5} )=9e^{-2,5} \) volt
Menghitung \( i_x \)
Arus yang mengalir melalui resistor 12 Ω dapat dicari menggunakan hukum Ohm:
\( i_x=\frac{v_x}{R}=\frac{9e^{-2,5}}{12}=\frac{9}{12 e^{-2,5}} \)
\( i_x=0,75e^{-2,5}\) ampere
Contoh soal 2
Perhatikan gambar di bawah ini:
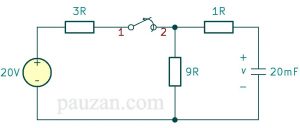
Gambar 8. Soal rangkaian RC orde satu
Dari gambar di atas, sakelar dalam kondisi tertutup (on) dalam jangka waktu yang lama, kemudian sakelar tersebut dibuka pada saat t=0. Carilah
- \( v(t) \) untuk t≥0
- energi awal yang tersimpan di dalam kapasitor
jawab
sumber tegangannya adalah DC artinya kapasitor bersifat sebagai rangkaian terbuka, rangkaian pada soal di atas menjadi:
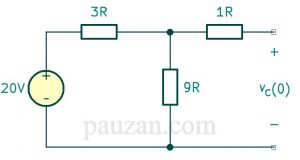
gambar 9. Bentuk lain dari rangkaian pada gambar 8
berdasarkan gambar 9, tegangan pada kapasitor \( v_C \) adalah sama besarnya dengan tegangan pada resistor 9 Ω. Kenapa resistor 1 Ω tidak dihitung? Karena tidak ada arus mengalir melewati kapasitor maka apakah ada resistor atau tidak tetap arus tidak bisa melewati kapasitor, artinya resistor 1 Ω juga dapat diganti dengan kabel atau dengan kata lain resistor tersebut dapat diabaikan. Tegangan pada 9 Ω dapat dicari menggunakan konsep pembagi tegangan, hasilnya adalah:
\( v_C=v_{9Ω}=\frac{9}{9+3} 20=15 \)V
Menghitung v untuk t≥0
Kemudian pada gambar 8, sakelar dibuka maka sekarang rangkaiannya menjadi:
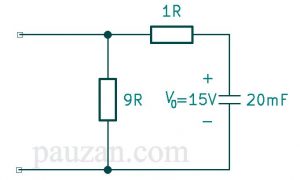
Gambar 10. Rangkaian setelah sakelar dibuka
Saat dibuka sakelar tersebut, saat itulah t=0, dengan menganggap pada t=0 tegangan pada kapasitor sebesar \(V_0=15 \)V, selanjutnya rangkaian pada gambar 10 dibuat bentuknya menjadi seperti pada gambar 1 yaitu hanya ada satu resistor dan kapasitor. Resistor 9 Ω dan 1 Ω tersusun seri maka:
\( R_s=9+1=10 Ω \)Kita bisa menghitung konstanta waktu τ:
\( τ=RC=R_s C=10 . 20 \times 10^{-3}=0,2 \)sekon
Oleh karena itu, dengan menggunakan persamaan (11) diperoleh tegangan pada kapasitor untuk t≥0 adalah:
\( v(t)=V_0 e^{-t}{τ}=15e^{\frac{-1}{0,2} t}\)\( v(t)=15e^{-5t} \)volt
Menghitung energi pada kapasitor
Energi awal (saat t=0) yang tersimpan pada kapasitor adalah:
\( w_C (0)=\frac{1}{2} Cv_c^2 (0)=\frac{1}{2}\times 20 \times 10^{-3} \times 15e^{-5(0)} \)\( w_C (0)=0,15e^0=0,15 \)joule
NEXT: Rangkaian RL Orde Satu