Rangkaian RL sumber bebas termasuk ke rangkaian orde satu.
Mari kita mulai pembahasan ini dengan menggunakan rangkaian seri antara induktor dengan resistor seperti pada gambar di bawah ini:
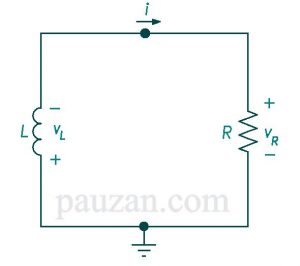
Gambar 1. Rangkaian RL sumber bebas
Pada saat t=0, arus pada induktor sebesar :
\( i(0)=I_0 \)………………………………………………………(1)
Energi yang tersimpan pada induktor saat t=0 adalah:
\( w(0)=\frac{1}{2} LI_0^2 \)…………………………………………..(2)
Kemudian menerapkan hukum tegangan Kirchhoff (KVL) pada gambar 1:
\( ΣV=0 \)\( v_L+v_R=0 \)………………………………………………..(3)
Mengingat \( v_L=L \frac{di}{dt} \) dan \( v_R=iR \), maka persamaan (3) menjadi:
\( L \frac{di}{dt}+Ri=0 \)Kedua ruas dibagi \( L \);
\( \frac{di}{dt}+\frac{R}{L} i=0 \)(R/L)i dipindah ke ruas kanan, maka:
\( \frac{di}{dt}=\frac{-R}{L} I \)…………………………..(4)
i dipindah ruas ke kiri dan dt ke ruas kanan, maka:
\( \frac{di}{i}=\frac{-R}{L} dt \)Kita integralkan kedua ruas:
\( \int_{I_0}^{i(t)}\frac{di}{i}=-\int_{0}^{t}\frac{R}{L}dt \)Ingat:
\( \int \frac{dx}{x}=\ln x \)Maka:
\( \ln i|_{0}^{i(t)}=-\frac{Rt}{L}|_0^t \) \( \ln i(t)-\ln I_0=-\frac{Rt}{L}+0 \)Ingat: ln a-ln b=ln a/b maka:
\( \ln \frac{i(t)}{I_0}=-\frac{Rt}{L} \)……………………………………….(5)
Bentuk di atas dapat diubah ke bentuk e:
\( e^{\ln \frac{i(t)}{I_0}}=e^{-\frac{Rt}{L}} \)Ingat \( e^{\ln a} =a \), dengan menganggap \(i(t)/I_0=a \)maka:
\( \frac{i(t)}{I_0}=e^{-\frac{Rt}{L}} \)
\( i(t)=I_0e^{-\frac{Rt}{L}} \)………………………………………..(6)
Persamaan (6) menunjukkan bahwa respon alami dari rangkaian RL adalah penurunan secara eksponensial dari arus mula-mulanya. Respon arus dapat dilihat pada gambar di bawah ini:
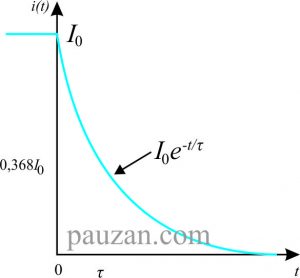
Gambar 2. Respon alami
Konstanta waktu bagi rangkaian RL adalah:
\( \tau =\frac{L}{R} \)………………………………………..(7)
Satuan τ adalah sekon. Persamaan (6) dapat juga ditulis:
\( i(t)=I_0e^{-\frac{t}{\tau}} \)……………………………………..(8)
Berapakah tegangan yang melalui resistor? Rumusnya adalah sebagai berikut:
\( v_R (t)=iR \)Dengan mensubtitusikan persamaan (8) maka diperoleh:
\( v_R(t)=I_0Re^{-\frac{t}{\tau}} \)…………………………………(9)
Sedangkan daya yang terdisipasi pada resistor sebesar:
\( p=v_R I \)Disubtitusikan persamaan (8) dan (9);
\( p=(I_0Re^{-\frac{t}{\tau}})(I_0e^{-\frac{t}{\tau}}) \)\( p=I_{0}^{2}Re^{-2t/\tau} \)………………………………………(10)
Energi yang diterima oleh resistor adalah:
\( w_R(t)=\int_{0}^{t}pdt=\int_{0}^{t}I_{0}^{2}Re^{-2t/\tau}dt \) \( w_R(t)=I_{0}^{2}R\int_{0}^{t}e^{-2t/\tau}dt \)Ingat:
\( \int e^{2x}dx=\frac{1}{2}e^{2x} \)Oleh karena itu:
\( w_R(t)=I_{0}^{2}R(-\frac{\tau}{2}e^{-2t/\tau})|_0^t=-\frac{\tau}{2}I_{0}^{2}R(e^{-2t/\tau}-e^0) \) \( w_R(t)=-\frac{\tau}{2}I_0^2R(e^{-2t/\tau}-1) \)τ=L/R maka;
\( w_R(t)=-\frac{1}{2}LI_0^2(e^{-2t/\tau}-1) \)\( w_R(t)=\frac{1}{2}LI_0^2(1-e^{-2t/\tau}) \)…………………………..(11)
Contoh soal 1
Perhatikan gambar di bawah ini:
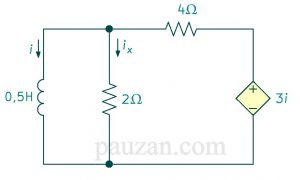
Gambar 3. Soal rangkaian RL sumber bebas
Jika \( i(0)=10 A \), hitunglah \( i(t) \) dan \( i_x \) pada rangkaian di atas
Jawab
Menghitung \( i(t) \)
Kita bisa menerapkan KVL seperti pada gambar berikut ini:
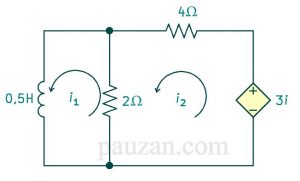
Gambar 4. Penerapakan KVL pada rangkaian
Loop 1;
\( Σv=0 \) \( v_L+v_{2Ω}=0 \) \( L\frac{di_1}{dt}+2(i_1-i_2)=0 \)Memasukkan nilai L;
\( \frac{1}{2}\frac{di_1}{dt}+2i_1-2i_2=0 \)Dikali 2;
\( \frac{di_1}{dt}+4i_1-4i_2=0 \)…………………………………..(12)
Loop 2:
\( Σv=0 \) \( 4i_2+2(i_2-i_1 )-3i_1=0 \) \( 6i_2-5i_1=0 \) \( i_2=\frac{5}{6} i_1 \)Disubtitusikan ke persamaan (12);
\( \frac{di_1}{dt}+4i_1-4(\frac{5}{6} i_1)=0 \) \( \frac{di_1}{dt}+4i_1-\frac{10}{3} i_1=0 \) \( \frac{di_1}{dt}+\frac{12-10}{3} i_1=0 \) \( \frac{di_1}{dt}=-\frac{2}{3}i_1 \)
\( i_1 \) dan \( dt \) dipindah ruas maka;
\( \frac{di_1}{i_1}=-\frac{2}{3}dt \)Kedua ruas kita integralkan:
\( \int_{i(0)}^{i(t)}\frac{di_1}{i_1}=\int_{0}^{t}-\frac{2}{3}dt \)Ingat;
\( \int \frac{dx}{x}=\ln x \)Maka:
\( \ln i_1|_{i(0)}^{i(t)}=-\frac{2}{3}t|_0^t \) \( \ln i(t)-\ln i(0)=-\frac{2}{3}t \)Ingat: ln a-ln b=ln a/b maka;
\( \ln \frac{i(t)}{i(0)}=-\frac{2}{3}t \)Diubah ke bentuk e:
\( e^{\ln \frac{i(t)}{i(0)}}=e^{-\frac{2}{3}t} \)Ingat: \( e^{\ln a} =a \) maka;
\( \frac {i(t)}{i(0)}=e^{-\frac{2}{3}t} \) \( i(t)=i(0)e^{-\frac{2}{3}t} \)Masukkan nilai i(0) maka;
\( i(t)=10e^{-(2/3)t}A \)
Menghitung \( i_x \)
Tegangan pada induktor adalah:
\( v_L=L\frac{di}{dt}=\frac{1}{2}\frac{d}{dt}(10e^{-(2/3)t}) \)\( v_L=5\frac{d}{dt}(e^{-(2/3)t})=5(-\frac{2}{3})e^{-(2/3)t} \)
\( v_L=-\frac{10}{3}e^{-(2/3)t}V \)
Karena induktor paralel dengan resistor 2 Ω maka tegangannya pun sama:
Arus yang melalui resistor adalah:
\( i_x=\frac{v_L}{R}=\frac {-\frac{10}{3}e^{-2/3)t}}{2} \)\( i_x=-1,667e^{-(2/3)t}A \)
Contoh soal 2
Perhatikan gambar di bawah ini:

Gambar 5. Soal rangkaian RL
Sakelar pada gambar di atas sudah lama tertutup, pada saat t=0, sakelar dibuka. Hitunglah \( i(t) \)untuk t>0.
Jawab
Saat t<0 sakelar dalam kondisi tertutup artinya inductor bersifat sebagai rangkaian pendek (short circuit) seperti yang ditunjukkan pada gambar di bawah ini:
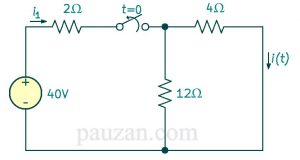
Gambar 6. Induktor yang bersifat sebagai rangkaian-pendek
Berdasarkan gambar 6, resistor 4 Ω dan 12 Ω tersusun paralel maka;
\( \frac{1}{R_p}=\frac{1}{4}+\frac{1}{12}=\frac{3+1}{12} \)\( R_p=3 Ω \)
Rangkaiannya menjadi:
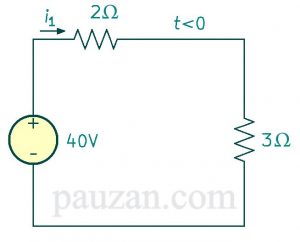
Gambar 7. Rangkaian setelah diparalelkan antara 4 dan 12 Ω
Susunan seri antara \( R_p \) dengan 2 Ω menghasilkan resistansi eqivalen:
\( R_{eq}=R_p+2=3+2=5 Ω \)Maka arus \( i_1 \) dapat diperoleh dengan hukum Ohm:
\( i_1=\frac{v}{R_{eq}} =\frac{4}{5}=8 A \)Selanjutnya mencari nilai i(t), perhatikan gambar 7, arus \( i_1 \) menemui percabangan sehingga arus i(t) dapat dicari menggunakan persamaan pada rangkaian pembagi arus:
\( i(t)=\frac{12}{12+4} i_1=\frac{3}{4}8=6 A \) , untuk \( t<0 \)
Arus pada induktor saat t=0 diasumsikan sama dengan saat t<0 maka;
\( i(0)=6 A \)
Saat sakelar dibuka maka rangkaian terbuka (t>0) seperti pada gambar di bawah ini:
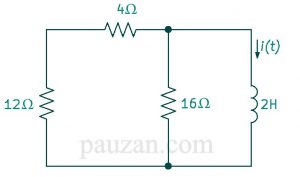
Gambar 8. Saat sakelar dibuka
Kita rubah bentuknya ke bentuk rangkaian RL sumber-bebas, dimana hanya ada satu R dan inductor. Maka:
Resistor 12 dan 4 Ω tersusun seri maka:
\( R_s=12+4=16 Ω \)Sekarang \( R_s \) paralel dengan 16 Ω, maka:
\( \frac{1}{R_{eq}} =\frac{1}{16}+\frac{1}{16}=\frac{2}{16} \) \( R_{eq}=8 Ω \)Menghitung konstanta waktu:
\( \tau=\frac{L}{R}=\frac{2}{8}=\frac{1}{4} sekon \)Arus yang melalui induktor adalah:
\( i(t)=i(0)e^{-t/\tau}=i(0)e^{-4t} \)\( i(t)=6e^{-4t} A \)
PREVIOUS: Rangkaian RC Orde Satu