Jika rangkaian seri RLC diberikan sumber DC secara tiba-tiba maka sumber DC tersebut bisa dimodelkan sebagai fungsi step dan reaksi dari rangkaian seri RLC disebut sebagai respon step. Perhatikan rangkaian di bawah ini:
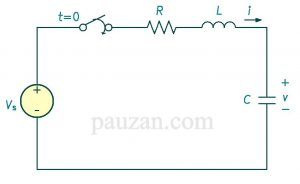
Gambar 1. Rangkaian RLC seri
Saat sakelar ditutup \( t=0 \) maka rangkaian akan memberikan respon step, kita coba terapkan hukum tegangan Kirchhoff (KVL) saat \( t>0 \);
\( \Sigma V=0 \) \( –V_s+V_R+V_L+V_C=0 \)
Tegangan masing-masing komponen:
\( V_R=Ri \)\( V_L=L \frac{di}{dt} \)
\( V_C=v \)
Maka;
\( –V_s+Ri+L \frac{di}{dt}+v=0 \)………………………………………..(1)
Nilai \( i \) adalah;
\( i=C \frac{dv}{dt} \)
Maka persamaan (1) menjadi:
\( –V_s+R(C \frac{dv}{dt})+L \frac{d(C \frac{dv}{dt})}{dt}+v=0 \)
\( C \) keluar dari penurunan maka;
\( LC \frac{d^2v}{dt^2}+RC \frac{dv}{dt}+v-V_s=0 \)
Kedua ruas dibagi \( LC \) maka;
\( \frac{d^2v}{dt^2}+\frac{R}{L}\frac{dv}{dt}+\frac{v}{LC}-\frac{V_s}{LC}=0 \)…………………(2)
Persamaan (2) adalah bentuk diferensial orde dua dari respon step rangkaian RLC seri. Perhatikan bahwa mesikpun diberikan sumber eksternal DC, karakteristik dari rangkaian RLC seri tidak berubah, jadi solusinya sama yaitu untuk kondisi overdamped, critically damped dan underdamped. Cuma yang berbeda hanyalah pada nilai konstanta \( A \) maupun \( s \). Solusi dari persamaan (2) adalah terdiri dari dua komponen yaitu respon transien dan respon steady-state:
\( v(t)=v_t(t)+v_{ss}(t) \)…………………………………………………(3)
Respon transien hanya beberapa saat, respon ini sama bentuknya dengan rangkaian RLC seri sumber bebas, maka respon transien pada RLC seri adalah sebagai berikut:
Overdamped:
\( v(t)=A_1 e^{s_1t}+A_2 e^{s_2t} \)……………………………………..(4)
Critically damped:
\( v(t)=(A_1+A_2t)e^{-\alpha t} \)………………………………………(5)
Catatan: \( s_1=s_2=-\alpha \)
Underdamped:
\( v_t(t)=(A_1 \cos \omega_{d}t+A_2 \sin \omega_{d}t)e^{-\alpha t} \)………………………..(6)
Respon steady state merupakan nilai akhir dari rangkaian, dimana pada saat itu terjadi tegangan kapasitor sama besarnya dengan sumber \( V_s \) maka:
\( v_{ss}=v(\infty)=V_s \)………………………………………………..(7)
Maka berdasarkan persamaan (3), kita cukup menambahkan tegangan \( V_s \) untuk tiap kondisi mulai dari overdamped, critically damped dan underdamped:
Overdamped:
\( v(t)=V-s+A_1 e^{s_1t}+A_2 e^{s_2t} \)……………………………………..(8)
Critically damped:
\( v(t)=V_s+(A_1+A_2t)e^{-\alpha t} \)………………………………………(9)
Catatan: \( s_1=s_2=-\alpha \)
Underdamped:
\( v_t(t)=V_s+(A_1 \cos \omega_{d}t+A_2 \sin \omega_{d}t)e^{-\alpha t} \)………………………..(10)
Contoh Soal
Perhatikan rangkaian berikut ini:
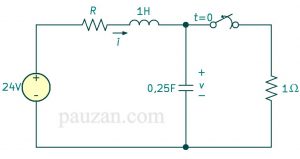
Gambar 2. Soal respon step dari rangkaian seri RLC
Tentukan \( v(t) \) dan \( i(t) \) untuk \( t>0 \), jika nilai \( R=5Ω, 4Ω, \) dan \( R=1Ω \)
Jawab
kondisi \( R=5Ω \)
Saat \( t<0 \) sakelar dalam kondisi tertutup dalam jangka waktu yang lama, maka rangkaian dalam kondisi steady state. Kapasitor bersifat sebagai rangkaian terbuka (open circuit) dan induktor bersifat sebagai hubung singkat (short circuit). Perhatikan rangkaian berikut:
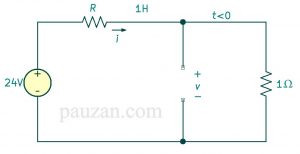
Gambar 3. Saat \( t<0 \), kapasitor bersifat terbuka, induktor bersifat hubung singkat
Berdasarkan gambar 3 dan membandingkannya dengan gambar 2, maka arus yang melalui induktor adalah sama saja dengan arus \( i \), maka:
\( i=\frac{V}{R_{eq}} \)
\( R_{eq} \) adalah rangkaian seri antara resistor 5Ω dengan 1Ω maka \( R_{eq}=5+1=6Ω \). Karena sesaat sebelum dan setelah sakelar dibuka, arus dalam induktor dianggap tetap maka:
\( i(0)=i(0^- )=i(0^+ )=\frac{24}{6}=4 A \)Perhatikan gambar 3, tegangan pada kapasitor sama besarnya dengan tegangan pada resistor 1Ω karena terhubung paralel. Sesaat sebelum dan sesaat setelah sakelar dibuka, tegangan pada kapasitor dianggap tetap maka:
\( v(0)=v(0^- )=v(0^+ )=iR \) \( v(0)=4 \times 1=4 V \)
Saat \( t>0 \)
Sakelar dibuka dan hubungam dengan resistor 1Ω terputus, maka rangkaiannya menjadi:
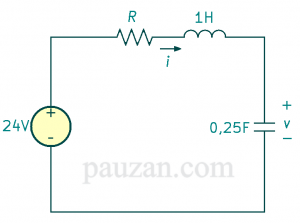
Gambar 4. Saat \( t>0 \), terbentuk rangkaian seri RLC
Kita menjumpai rangkaian seri RLC, langkah pertama adalah meneetukan \(\alpha \) dan \( \omega_{0} \)
\( \alpha=\frac{R}{2L}=\frac{5}{2\times 1}=2,5 \) \( \omega_{0}=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{1\times 0,25} }=2 \)
Diperoleh \( \alpha >\omega_{0} \) maka termasuk ke dalam overdamped.
\( v(t)=V_s+A_1 e^{s_1 t}+A_2 e^{s_2 t} \)
Dari persamaan di atas, yang belum diketahui adalah \( A_1,A_2, s_1, s_2 \).
Mencari \( s_{1,2} \)
\( s_1=-\alpha +\sqrt{\alpha^2-\omega_{0}^{2}}=-2,5+\sqrt{6,25-4} \) \( s_1=-2,5+1,5=-1 \)
Dengan cara yang sama, \( s_2 \);
\( s_2=-\alpha -\sqrt{\alpha^2-\omega_{0}^{2}}=-2,5-\sqrt{6,25-4} \) \( s_2=-2,5-1,5=-4 \)
Mencari \( A_1 \) dan \( A_2 \):
Kita gunakan kondisi awal yaitu saat \( t=0 \), tegangannya adalah:
\( v(t)=24+A_1 e^{-t}+A_2 e^{-4t} \)\( v(0)=24+A_1 e^{0}+A_2 e^{0} \)
\( v(0)=24+A_1+A_2 \)
Kita sudah mendapatkan \( v(0)=4 \) V, maka;
\( 4=24+A_1+A_2 \)\( A_1=-A_2-20 \)
Kita turunkan tegangan terhadap waktu:
\( \frac{dv}{dt}=\frac{d}{dt}(24+A_1 e^{-t}+A_2 e^{-4t} ) \)\( \frac{dv}{dt} =-A_1 e^{-t}-4A_2 e^{-4t} \)
Saat \( t=0 \);
\( \frac{ dv(0)}{dt}=-A_1 e^0-4A_2 e^0 \)\( \frac{ dv(0)}{dt}=-A_1-4A_2 \)
Mencari \( dv(0)/dt \);
Persamaan arus paa kapasitor adalah:
\( i=C \frac{dv}{dt} \)Maka;
\( \frac{dv}{dt}=\frac{i}{C} \)
Saat \( t=0 \);
\( \frac{ dv(0)}{dt}=\frac{ i(0)}{C} \)Kita sudah mendapatkan \( i(0)=4 \) A maka:
\( \frac{dv(0)}{dt}=\frac{4}{0,25} =16 \)Maka:
\( 16=-A_1-4A_2 \)
Kita subtitusikan persamaan \( A_1 \);
\( 16=-(-A_2-20)-4A_2 \) \( 16=A_2-4A_2+20 \) \( A_2=\frac{-4}{-3}=1,33 \)Nilai \( A_1 \);
\( A_1=-(1,33)-20=-21,33 \)Kita sudah mendapatkan semua variabel yang belum diketahui, maka persamaan tegangannya adalah:
\( v(t)=24-21,33e^{-t}+1,33e^{-4t} \)
Menentukan \( i(t) \)
Arus pada induktor adalah sama saja dengan arus yang mengalir pada resistor \( 5Ω \) atau arus pada kapasitor karena induktor bersifat hubung singkat. Persamaan arus pada kapasitor adalah:
\( i=C \frac{dv}{dt} \)Subtitusi persamaan tegangan:
\( i(t)=C \frac{d}{dt} (24-21,33e^{-t}+1,33e^{-4t} ) \)\( i(t)=0,25(21,33e^{-t}-5,32e^{-4t} ) \)
\( i(t)=5,3325e^{-t}-1,33e^{-4t} A \)
Kondisi \( R=4Ω \)
Saat \( t<0 \), rangkaiannya sama dengan gambar 3 di atas, yang berbeda hanya nilai \( R \) saja. Kita hitung arus \( i(0) \), konsepnya sama dengan kondisi pertama yang diganti adalah nilai \( R \) yang sebelumnya \( 5Ω \) kini menjadi 4Ω.
\( i(0)=\frac{24}{4+1}=4,8 A \)maka tegangan awal kapasitor adalah:
\( v(0)=iR=4,8 \times 1=4,8 V \)
Mencari \( \alpha \)
\( \alpha=\frac{R}{2L}=\frac{4}{2\times 1} =2 \)Sedangkan \( \omega_{0} \) nilainya tetap yaitu sebesar 2. Pada kasus ini \( \alpha=\omega_{0} \) artinya berada pada kondisi critically damped. Persamaan untuk penyelesaiannya adalah:
\( v(t)=V_s+(A_1+A_2 t) e^{-\alpha t} \)
Kita sudah mengetahui \( V_s \) dan \( \alpha \), maka yang akan dicari adalah \( A_1 \) dan \( A_2 \).
Mencari \( A_1 \) dan \( A_2 \)
Kita gunakan kondisi awal pada persamaan tegangan di atas:
\( v(0)=24+(A_1+A_2 (0)) e^{-2(0)} \)\( v(0)=24+A_1 \)
Subtitusikan \( v(0)=4,8 \)V, maka;
\( A_1=4,8-24=-19,2 \)Selanjutnya persamaan tegangan diturunkan terhadap waktu:
\( \frac{dv}{dt}=\frac{d}{dt} (24+(A_1+A_2 t) e^{-2t} ) \)\( \frac{dv}{dt}=(A_2 ) e^{-2t}+(A_1+A_2 t)(-2) e^{-2t} \)
\( \frac{dv}{dt}=(-2A_1+A_2-2A_2 t) e^{-2t} \)
Saat \( t=0 \);
\( \frac{dv(0)}{dt}=(-2A_1+A_2+0) e^0 \)\( \frac{dv(0)}{dt}=-2A_1+A_2 \)
Mencari \( dv(0)/dt \);
Persamaan arus pada kapasitor adalah:
\( i(t)=C \frac{dv(t)}{dt} \)\( \frac{dv(t)}{dt}=\frac{i(t)}{C} \)
Saat \( t=0 \);
\( \frac{dv(0)}{dt}=\frac{i(0)}{C} \)
Subtitusikan \( i(0)=4,8 \)A maka;
\( \frac{dv(0)}{dt}=\frac{4,8}{0,25} =19,2 \)
Jadi persamaan \( dv(0)/dt \) menjadi;
\( 19,2=-2A_1+A_2 \)
Subtitusi \( A_1=-19,2 \);
\( A_2=19,2+2(-19,2)=-19,2 \)Jadi kita sudah mendapatkan nilai dari semua variabel yang belum diketahui, maka persamaan solusinya adalah:
\( v(t)=24+(-19,2-19,2t) e^{-2t} \)\( v(t)=24-19,2(1+t) e^{-2t} V \)
Mencari \( i(t) \)
Persamaan arus pasti berasal dari arus induktor, mengingat arus pada induktor sama dengan arus arus ke kapasitor maka kita dapat menggunakan persamaan arus pada kapasitor:
\( i(t)=C \frac{dv}{dt} \)Kita turunkan \( v \) terhadapt \( t \):
\( i(t)=0,25 \frac{d}{dt} (24-19,2(1+t) e^{-2t} ) \)\( i(t)=0,25 \frac{d}{dt}[24-19,2e^{-2t}-19,2te^{-2t} ] \)
\( i(t)=0,25[(-19,2)(-2) e^{-2t}-19,2{(e^{-2t} )+(t(-2) e^{-2t} )}] \) \( i(t)=0,25[38,4e^{-2t}-19,2e^{-2t}+38,4te^{-2t} ] \)
\( i(t)=4,8e^{-2t}+9,6te^{-2t} \)
Kondisi \( R=1Ω \)
Saat \( t<0 \), rangkaiannya sama dengan gambar 3 di atas, yang berbeda hanya nilai \( R \) saja. Kita hitung arus \( i(0) \), konsepnya sama dengan kondisi pertama dan kedua yang diganti adalah nilai \( R \).
\( i(0)=\frac{24}{1+1}=12 A \)maka tegangan awal kapasitor adalah:
\( v(0)=iR=12\times 1=12 V \)
Mencari \( \alpha \)
\( \alpha=\frac{R}{2L}=\frac{1}{2\times 1}=0,5 \)Sedangkan \( \omega_{0} \) nilainya tetap yaitu sebesar 2. Pada kasus ini \( \alpha<\omega_{0} \) artinya berada pada kondisi underdamped. Persamaan untuk penyelesaiannya adalah:
\( v(t)=V_s+(A_1 \cos \omega_{d} t+A_2 \sin \omega_{d} t ) e^{-\alpha t} \)
Variabel yang belum dikaetahui adalah \( A_1, A_2 \) dan \( \omega_{d} \).
Mencari \( \omega_{d} \):
\( \omega_{d}=\sqrt{\omega_{0}^{2}-\alpha^2 }=\sqrt{4-0,25} \)\( \omega_{d}=\sqrt{3,75}=1,936 \)
Persamaan responnya menjadi:
\( v(t)=24+(A_1 \cos 1,96t+A_2 \sin 1,936t)e^{-0,5t} \)
Mencari \( A_1 \) dan \( A_2 \)
Pada saat \( t=0 \), persamaan tegangan menjadi:
\( v(0)=24+(A_1 \cos 0 +A_2 \sin 0)e^{0} \)\( v(0)=24+A_1 \)
Kita subtitusi \( v(0)=12 V \), maka:
\( A_1=12-24=-12 \)Untuk mencari \( A_2 \) kita turunkan persamaan tegangan terhadap waktu:
\( \frac{dv}{dt}=\frac{d}{dt}[(24+(A_1 \cos 1,936t+A_2 \sin 1,936t))e^{-0,5t} ] \)\( \frac{dv}{dt}=(-1,936A_1 \sin 1,936t+1,936A_2 \cos 1,936t)e^{-0,5t} +(A_1 \cos 1,936t+A_2 \sin 1,936t)(-0,5)e^{-0,5t} \)
Saat \( t=0 \), semua sinus bernilai 0, \( e^0=1 \) maka;
\( \frac{dv(0)}{dt}=(1,936A_2-0,5A_1) \)
Mencari \( dv(0)/dt \):
Persamaan arus pada kapasitor adalah:
\( i(0)=C \frac{dv(0)}{dt} \)
Maka;
\( \frac{dv(0)}{dt}=\frac{i(0)}{C} \)
Kita sudah mendapatkan \( i(0)=12 A \) dan \( C=0,25 F \), maka;
\( \frac{dv(0)}{dt}=\frac{12}{0,25}=48 \)
Jadi;
\( 48=1,936A_2-0,5A_1 \)Dimasukkan \( A_1=-12 \);
\( 1,936A_2=48+0,5(-12)=48-6 \)\( A_2=\frac{42}{1,936}=21,694 \)
Kita sudah mendapatkan semua variabel yang belum diketahui, maka persamaan tegangannya adalah:
\( v(t)=24+(-12 \cos 1,936t+21,694 \sin 1,936t)e^{-0,5t} \)\( v(t)=24+(21,694 \sin 1,936t-12 \cos 1,936t)e^{-0,5t} \)
Mencari \( i(t) \)
Persamaan arus yang digunakan adalah arus pada kapasitor karena arus tersebut sama besarnya dengan arus yang melalui induktor:
\( i(t)=C \frac{dv(t)}{dt} \) \( i(t)=0,25 \frac{d}{dt}[24+(21,694 \sin 1,936t-12 \cos 1,936t)e^{-0,5t} ] \) \( i(t)=(3,1 \sin 1,936t+12 \cos 1,936t)e^{-0,5t} A \)
Perhatikan grafik dari ketiga kondisi di atas pada gambar di bawah ini:
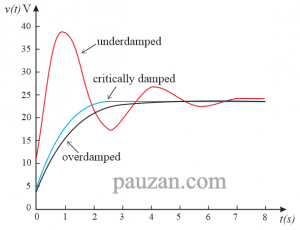
Gambar 5. Grafik kondisi overdamped, critically damped dan underdamped
PREVIOUS: Rangkaian RLC paralel
NEXT: Respon Step RLC Paralel